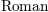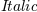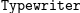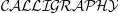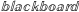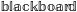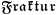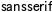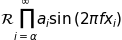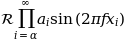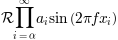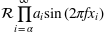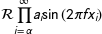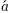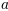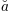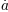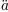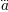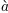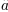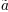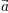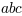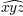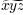Escrevendo expressões matemáticas

Você pode usar um subconjunto de marcação TeX em qualquer string de texto Matplotlib colocando-o dentro de um par de cifrões ($).

Observe que você não precisa ter o TeX instalado, pois o Matplotlib fornece seu próprio analisador de expressão TeX, mecanismo de layout e fontes. O mecanismo de layout é uma adaptação bastante direta dos algoritmos de layout no TeX de Donald Knuth, então a qualidade é muito boa (o Matplotlib também oferece uma usetex opção para aqueles que desejam chamar o TeX para gerar seu texto; consulte Renderização de texto com LaTeX ) .

Qualquer elemento de texto pode usar texto matemático. Você deve usar strings brutas (antes das aspas com um 'r') e cercar o texto matemático com cifrões ($), como no TeX. Texto regular e texto matemático podem ser intercalados na mesma string. Mathtext pode usar DejaVu Sans (padrão), DejaVu Serif, as fontes Computer Modern (de (La)TeX), fontes STIX (que são projetadas para combinar bem com Times) ou uma fonte Unicode fornecida por você. A fonte mathtext pode ser selecionada via rcParams["mathtext.fontset"](padrão: 'dejavusans') (consulte Personalizando Matplotlib com folhas de estilo e rcParams )

Aqui está um exemplo simples:

# plain text
plt.title('alpha > beta')

produz "alfa > beta".

Considerando que:

# math text
plt.title(r'$\alpha > \beta$')

produz " ".

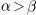Observação

Mathtext deve ser colocado entre um par de cifrões ($). Para facilitar a exibição de valores monetários, por exemplo, "$ 100,00", se um único cifrão estiver presente em toda a string, ele será exibido textualmente como um cifrão. Esta é uma pequena mudança em relação ao TeX normal, onde o cifrão em texto não matemático teria que ser escapado ('\$').

Observação

Enquanto a sintaxe dentro do par de cifrões ($) visa ser semelhante ao TeX, o texto fora não. Em particular, personagens como:

# $ % & ~ _ ^ \ { } \( \) \[ \]

têm um significado especial fora do modo matemático no TeX. Portanto, esses caracteres se comportarão de maneira diferente dependendo de rcParams["text.usetex"](padrão: False). Consulte o tutorial usetex para obter mais informações.

Subscritos e sobrescritos

Para criar subscritos e sobrescritos, use os símbolos '_'e :'^'

r'$\alpha_i > \beta_i$'

\[\alpha_i > \beta_i\]

Para exibir subscritos ou sobrescritos com várias letras corretamente, você deve colocá-los entre chaves {...}:

r'$\alpha^{ic} > \beta_{ic}$'

\[\alpha^{ic} > \beta_{ic}\]

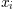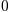Alguns símbolos colocam automaticamente seus subscritos/sobrescritos abaixo e acima do operador. Por exemplo, para escrever a soma de de a 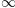, você poderia fazer:

r'$\sum_{i=0}^\infty x_i$'

\[\sum_{i=0}^\infty x_i\]

Frações, binômios e números empilhados

Frações, binômios e números empilhados podem ser criados com os comandos , e, \frac{}{}respectivamente \binom{}{}:\genfrac{}{}{}{}{}{}

r'$\frac{3}{4} \binom{3}{4} \genfrac{}{}{0}{}{3}{4}$'

produz

\[\frac{3}{4} \binom{3}{4} \genfrac{}{}{0pt}{}{3}{4}\]

As frações podem ser aninhadas arbitrariamente:

r'$\frac{5 - \frac{1}{x}}{4}$'

produz

\[\frac{5 - \frac{1}{x}}{4}\]

Observe que é necessário ter cuidado especial ao colocar parênteses e colchetes em torno de frações. Fazer as coisas da maneira óbvia produz parênteses muito pequenos:

r'$(\frac{5 - \frac{1}{x}}{4})$'

\[(\frac{5 - \frac{1}{x}}{4})\]

A solução é preceder o colchete com \lefte \rightinformar ao analisador que esses colchetes abrangem todo o objeto.:

r'$\left(\frac{5 - \frac{1}{x}}{4}\right)$'

\[\left(\frac{5 - \frac{1}{x}}{4}\right)\]

Radicais

Os radicais podem ser produzidos com o \sqrt[]{}comando. Por exemplo:

r'$\sqrt{2}$'

\[\sqrt{2}\]

Qualquer base pode (opcionalmente) ser fornecida entre colchetes. Observe que a base deve ser uma expressão simples e não pode conter comandos de layout como frações ou sub/sobrescritos:

r'$\sqrt[3]{x}$'

\[\sqrt[3]{x}\]

Fontes

A fonte padrão é itálico para símbolos matemáticos.

Observação

Esse padrão pode ser alterado usando rcParams["mathtext.default"](padrão: 'it'). Isso é útil, por exemplo, para usar a mesma fonte que o texto normal não matemático para texto matemático, definindo-o como regular.

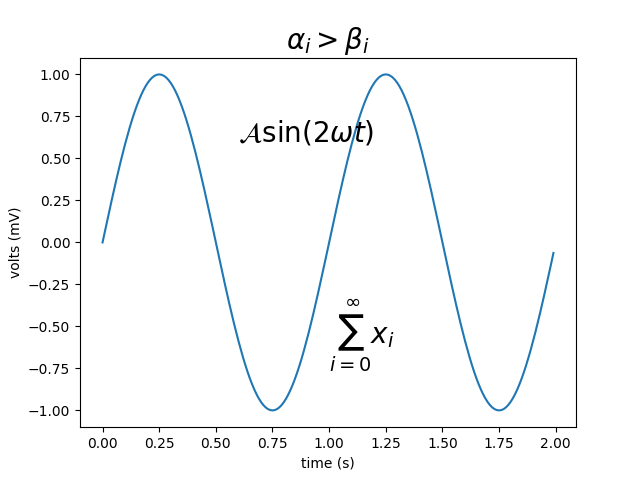
Para alterar as fontes, por exemplo, para escrever "pecado" em uma fonte romana, inclua o texto em um comando de fonte:

r'$s(t) = \mathcal{A}\mathrm{sin}(2 \omega t)$'

\[s(t) = \mathcal{A}\mathrm{sin}(2 \omega t)\]

Mais convenientemente, muitos nomes de funções comumente usados ​​que são compostos em uma fonte romana têm atalhos. Assim, a expressão acima poderia ser escrita da seguinte forma:

r'$s(t) = \mathcal{A}\sin(2 \omega t)$'

\[s(t) = \mathcal{A}\sin(2 \omega t)\]

Aqui, "s" e "t" são variáveis ​​em fonte itálica (padrão), "sin" está em fonte romana e a amplitude "A" está em fonte caligráfica. Observe que, no exemplo acima, a caligrafia Aé compactada no formato sin. Você pode usar um comando de espaçamento para adicionar um pouco de espaço em branco entre eles:

r's(t) = \mathcal{A}\/\sin(2 \omega t)'

\[s(t) = \mathcal{A}\,\sin(2 \omega t)\]

As opções disponíveis com todas as fontes são:

Comando	Resultado
\mathrm{Roman}
\mathit{Italic}
\mathtt{Typewriter}
\mathcal{CALLIGRAPHY}

Ao usar as fontes STIX , você também tem a opção de:

Comando	Resultado
\mathbb{blackboard}
\mathrm{\mathbb{blackboard}}
\mathfrak{Fraktur}
\mathsf{sansserif}
\mathrm{\mathsf{sansserif}}

Há também cinco "conjuntos de fontes" globais para escolher, que são selecionados usando o mathtext.fontsetparâmetro em matplotlibrc .

dejavusans: DejaVu Sans

dejavuserif: DejaVu Serif

cm: Computador Moderno (TeX)

stix: STIX (projetado para combinar bem com Times)

stixsans: STIX sem serifa

Além disso, você pode usar \mathdefault{...}ou seu alias \mathregular{...}para usar a fonte usada para texto normal fora do texto matemático. Há uma série de limitações para essa abordagem, principalmente porque muito menos símbolos estarão disponíveis, mas pode ser útil fazer com que as expressões matemáticas se misturem bem com outro texto no gráfico.

Fontes personalizadas

mathtext também fornece uma maneira de usar fontes personalizadas para matemática. Esse método é bastante complicado de usar e deve ser considerado um recurso experimental apenas para usuários pacientes. Definindo rcParams["mathtext.fontset"](padrão: 'dejavusans') como custom, você pode definir os seguintes parâmetros, que controlam qual arquivo de fonte usar para um determinado conjunto de caracteres matemáticos.

Parâmetro	Corresponde a
mathtext.it	\mathit{}ou itálico padrão
mathtext.rm	\mathrm{}Romana (vertical)
mathtext.tt	\mathtt{}Máquina de escrever (monoespacial)
mathtext.bf	\mathbf{}negrito itálico
mathtext.cal	\mathcal{}caligráfico
mathtext.sf	\mathsf{}sem serifa

Cada parâmetro deve ser definido como um descritor de fonte fontconfig (conforme definido no capítulo sobre fontes ainda a ser escrito).

As fontes usadas devem ter um mapeamento Unicode para encontrar quaisquer caracteres não latinos, como o grego. Se você quiser usar um símbolo matemático que não esteja contido em suas fontes personalizadas, você pode definir rcParams["mathtext.fallback"](padrão: 'cm') como 'cm', 'stix'ou 'stixsans' o que fará com que o sistema de texto matemático use caracteres de uma fonte alternativa sempre que um caractere específico não puder ser encontrado em a fonte personalizada.

Observe que os glifos matemáticos especificados em Unicode evoluíram com o tempo e muitas fontes podem não ter glifos no lugar correto para texto matemático.

Acentos

Um comando de acento pode preceder qualquer símbolo para adicionar um acento acima dele. Existem formulários longos e curtos para alguns deles.

Comando	Resultado
\acute aou\'a
\bar a
\breve a
\dot aou\.a
\ddot aou\''a
\dddot a
\ddddot a
\grave aou\`a
\hat aou\^a
\tilde aou\~a
\vec a
\overline{abc}

Além disso, existem dois acentos especiais que se ajustam automaticamente à largura dos símbolos abaixo:

Comando	Resultado
\widehat{xyz}
\widetilde{xyz}

Deve-se tomar cuidado ao colocar acentos em i's e j's minúsculos. Observe que a seguir \imathé usado para evitar o ponto extra sobre o i:

r"$\hat i\ \ \hat \imath$"

\[\hat i\ \ \hat \imath\]

Símbolos

Você também pode usar um grande número de símbolos TeX, como em \infty, \leftarrow, \sum, \int.

grego minúsculo

α\alpha	β\beta	χ\chi	δ\delta	ϝ\digamma	ε\epsilon
η\eta	γ\gamma	ι\iota	κ\kappa	λ\lambda	μ\mu
ν\nu	ω\omega	ϕ\phi	π\pi	ψ\psi	ρ\rho
σ\sigma	τ\tau	θ\theta	υ\upsilon	ε\varepsilon	ϰ\varkappa
φ\varphi	ϖ\varpi	ϱ\varrho	ς\varsigma	ϑ\vartheta	ξ\xi
ζ\zeta

Grego maiúsculo

Δ\Delta	Γ\Gamma	Λ\Lambda	Ω\Omega	Φ\Phi	Π\Pi	Ψ\Psi	Σ\Sigma
Θ\Theta	Υ\Upsilon	Ξ\Xi	℧\mho	∇\nabla

hebraico

ℵ\aleph

ℶ\beth

ℸ\daleth

ℷ\gimel

Delimitadores

//	[[	⇓\Downarrow	⇑\Uparrow	‖\Vert	\\backslash
↓\downarrow	⟨\langle	⌈\lceil	⌊\lfloor	⌞\llcorner	⌟\lrcorner
⟩\rangle	⌉\rceil	⌋\rfloor	⌜\ulcorner	↑\uparrow	⌝\urcorner
|\vert	{\{	|\|	}\}	]]	||

símbolos grandes

⋂\bigcap	⋃\bigcup	⨀\bigodot	⨁\bigoplus	⨂\bigotimes	⨄\biguplus
⋁\bigvee	⋀\bigwedge	∐\coprod	∫\int	∮\oint	∏\prod
∑\sum

Nomes de função padrão

Pr\Pr	arcos\arccos	arcsin\arcsin	arctan\arctan	arg\arg	porque\cos
cosh\cosh	berço\cot	coth\coth	csc\csc	grau\deg	det\det
escurecer\dim	exp\exp	gcd\gcd	hom\hom	inf\inf	ker\ker
lg\lg	lim\lim	limite\liminf	limsup\limsup	ln\ln	registro\log
máximo\max	min\min	segundo\sec	pecado\sin	sinh\sinh	e aí?\sup
bronzeado\tan	tanh\tanh

Operação binária e símbolos de relação

≎\Bumpeq	⋒\Cap	⋓\Cup	≑\Doteq
⨝\Join	⋐\Subset	⋑\Supset	⊩\Vdash
⊪\Vvdash	≈\approx	≊\approxeq	∗\ast
≍\asymp	϶\backepsilon	∽\backsim	⋍\backsimeq
⊼\barwedge	∵\because	≬\between	○\bigcirc
▽\bigtriangledown	△\bigtriangleup	◀\blacktriangleleft	▶\blacktriangleright
⊥\bot	⋈\bowtie	⊡\boxdot	⊟\boxminus
⊞\boxplus	⊠\boxtimes	∙\bullet	≏\bumpeq
∩\cap	⋅\cdot	∘\circ	≗\circeq
≔\coloneq	≅\cong	∪\cup	⋞\curlyeqprec
⋟\curlyeqsucc	⋎\curlyvee	⋏\curlywedge	†\dag
⊣\dashv	‡\ddag	⋄\diamond	÷\div
⋇\divideontimes	≐\doteq	≑\doteqdot	∔\dotplus
⌆\doublebarwedge	≖\eqcirc	≕\eqcolon	≂\eqsim
⪖\eqslantgtr	⪕\eqslantless	≡\equiv	≒\fallingdotseq
⌢\frown	≥\geq	≧\geqq	⩾\geqslant
≫\gg	⋙\ggg	⪺\gnapprox	≩\gneqq
⋧\gnsim	⪆\gtrapprox	⋗\gtrdot	⋛\gtreqless
⪌\gtreqqless	≷\gtrless	≳\gtrsim	∈\in
⊺\intercal	⋋\leftthreetimes	≤\leq	≦\leqq
⩽\leqslant	⪅\lessapprox	⋖\lessdot	⋚\lesseqgtr
⪋\lesseqqgtr	≶\lessgtr	≲\lesssim	≪\ll
⋘\lll	⪹\lnapprox	≨\lneqq	⋦\lnsim
⋉\ltimes	∣\mid	⊧\models	∓\mp
⊯\nVDash	⊮\nVdash	≉\napprox	≇\ncong
≠\ne	≠\neq	≠\neq	≢\nequiv
≱\ngeq	≯\ngtr	∋\ni	≰\nleq
≮\nless	∤\nmid	∉\notin	∦\nparallel
⊀\nprec	≁\nsim	⊄\nsubset	⊈\nsubseteq
⊁\nsucc	⊅\nsupset	⊉\nsupseteq	⋪\ntriangleleft
⋬\ntrianglelefteq	⋫\ntriangleright	⋭\ntrianglerighteq	⊭\nvDash
⊬\nvdash	⊙\odot	⊖\ominus	⊕\oplus
⊘\oslash	⊗\otimes	∥\parallel	⟂\perp
⋔\pitchfork	±\pm	≺\prec	⪷\precapprox
≼\preccurlyeq	≼\preceq	⪹\precnapprox	⋨\precnsim
≾\precsim	∝\propto	⋌\rightthreetimes	≓\risingdotseq
⋊\rtimes	∼\sim	≃\simeq	∕\slash
⌣\smile	⊓\sqcap	⊔\sqcup	⊏\sqsubset
⊏\sqsubset	⊑\sqsubseteq	⊐\sqsupset	⊐\sqsupset
⊒\sqsupseteq	⋆\star	⊂\subset	⊆\subseteq
⫅\subseteqq	⊊\subsetneq	⫋\subsetneqq	≻\succ
⪸\succapprox	≽\succcurlyeq	≽\succeq	⪺\succnapprox
⋩\succnsim	≿\succsim	⊃\supset	⊇\supseteq
⫆\supseteqq	⊋\supsetneq	⫌\supsetneqq	∴\therefore
×\times	⊤\top	◁\triangleleft	⊴\trianglelefteq
≜\triangleq	▷\triangleright	⊵\trianglerighteq	⊎\uplus
⊨\vDash	∝\varpropto	⊲\vartriangleleft	⊳\vartriangleright
⊢\vdash	∨\vee	⊻\veebar	∧\wedge
≀\wr

símbolos de seta

⇓\Downarrow	⇐\Leftarrow	⇔\Leftrightarrow	⇚\Lleftarrow
⟸\Longleftarrow	⟺\Longleftrightarrow	⟹\Longrightarrow	↰\Lsh
⇗\Nearrow	⇖\Nwarrow	⇒\Rightarrow	⇛\Rrightarrow
↱\Rsh	⇘\Searrow	⇙\Swarrow	⇑\Uparrow
⇕\Updownarrow	↺\circlearrowleft	↻\circlearrowright	↶\curvearrowleft
↷\curvearrowright	⤎\dashleftarrow	⤏\dashrightarrow	↓\downarrow
⇊\downdownarrows	⇃\downharpoonleft	⇂\downharpoonright	↩\hookleftarrow
↪\hookrightarrow	⇝\leadsto	←\leftarrow	↢\leftarrowtail
↽\leftharpoondown	↼\leftharpoonup	⇇\leftleftarrows	↔\leftrightarrow
⇆\leftrightarrows	⇋\leftrightharpoons	↭\leftrightsquigarrow	↜\leftsquigarrow
⟵\longleftarrow	⟷\longleftrightarrow	⟼\longmapsto	⟶\longrightarrow
↫\looparrowleft	↬\looparrowright	↦\mapsto	⊸\multimap
⇍\nLeftarrow	⇎\nLeftrightarrow	⇏\nRightarrow	↗\nearrow
↚\nleftarrow	↮\nleftrightarrow	↛\nrightarrow	↖\nwarrow
→\rightarrow	↣\rightarrowtail	⇁\rightharpoondown	⇀\rightharpoonup
⇄\rightleftarrows	⇄\rightleftarrows	⇌\rightleftharpoons	⇌\rightleftharpoons
⇉\rightrightarrows	⇉\rightrightarrows	↝\rightsquigarrow	↘\searrow
↙\swarrow	→\to	↞\twoheadleftarrow	↠\twoheadrightarrow
↑\uparrow	↕\updownarrow	↕\updownarrow	↿\upharpoonleft
↾\upharpoonright	⇈\upuparrows

Símbolos diversos

$\$	UMA\AA	Ⅎ\Finv	⅁\Game
ℑ\Im	¶\P	ℜ\Re	§\S
∠\angle	‵\backprime	★\bigstar	■\blacksquare
▴\blacktriangle	▾\blacktriangledown	⋯\cdots	✓\checkmark
®\circledR	Ⓢ\circledS	♣\clubsuit	∁\complement
©\copyright	⋱\ddots	♢\diamondsuit	ℓ\ell
∅\emptyset	ð\eth	∃\exists	♭\flat
∀\forall	ħ\hbar	♡\heartsuit	ℏ\hslash
∭\iiint	∬\iint	eu\imath	∞\infty
ȷ\jmath	…\ldots	∡\measuredangle	♮\natural
¬\neg	∄\nexists	∰\oiiint	∂\partial
′\prime	♯\sharp	♠\spadesuit	∢\sphericalangle
ß\ss	▿\triangledown	∅\varnothing	▵\vartriangle
⋮\vdots	℘\wp	¥\yen

Se um símbolo específico não tiver um nome (como é o caso de muitos dos símbolos mais obscuros nas fontes STIX), os caracteres Unicode também podem ser usados:

r'$\u23ce$'

Exemplo

Aqui está um exemplo que ilustra muitos desses recursos no contexto.