Observação
Clique aqui para baixar o código de exemplo completo
Normalização do mapa de cores #
Os objetos que usam mapas de cores por padrão mapeiam linearmente as cores no mapa de cores dos valores de dados vmin a vmax . Por exemplo:
mapeará os dados em Z linearmente de -1 a +1, então Z=0 dará uma cor no centro do mapa de cores RdBu_r (branco neste caso).
Matplotlib faz esse mapeamento em duas etapas, com uma normalização dos dados de entrada para [0, 1] ocorrendo primeiro e, em seguida, mapeando os índices no mapa de cores. Normalizações são classes definidas no
matplotlib.colors()módulo. A normalização linear padrão é matplotlib.colors.Normalize().
Artistas que mapeiam dados para cores passam os argumentos vmin e vmax para construir uma matplotlib.colors.Normalize()instância e então a chamam:
In [1]: import matplotlib as mpl
In [2]: norm = mpl.colors.Normalize(vmin=-1, vmax=1)
In [3]: norm(0)
Out[3]: 0.5
No entanto, às vezes há casos em que é útil mapear dados para mapas de cores de maneira não linear.
Logarítmico #
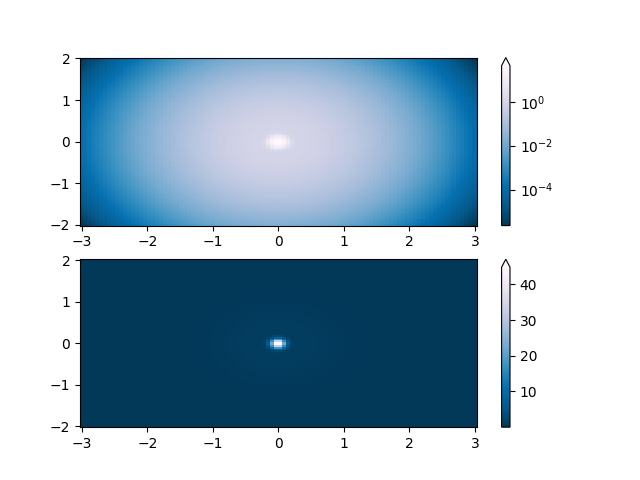
Uma das transformações mais comuns é plotar os dados tomando seu logaritmo (na base 10). Essa transformação é útil para exibir alterações em escalas diferentes. Usando colors.LogNormnormaliza os dados via
\(log_{10}\). No exemplo abaixo, há duas saliências, uma bem menor que a outra. Usando colors.LogNorm, a forma e a localização de cada saliência podem ser vistas claramente:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cbook as cbook
from matplotlib import cm
N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
# A low hump with a spike coming out of the top right. Needs to have
# z/colour axis on a log scale so we see both hump and spike. linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolor(X, Y, Z,
norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()
Centralizado #
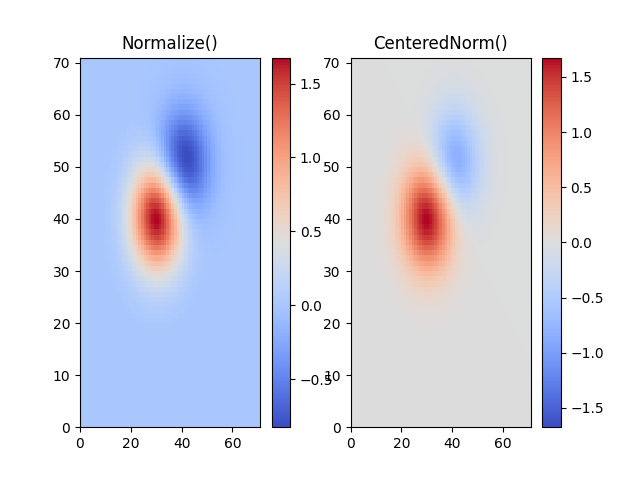
Em muitos casos, os dados são simétricos em torno de um centro, por exemplo, anomalias positivas e negativas em torno de um centro 0. Nesse caso, gostaríamos que o centro fosse mapeado para 0,5 e o ponto de dados com o maior desvio do centro fosse mapeado para 1,0, se seu valor for maior que o centro, ou 0,0 caso contrário. A norma colors.CenteredNormcria esse mapeamento automaticamente. É adequado para ser combinado com um mapa de cores divergente que usa bordas de cores diferentes que se encontram no centro em uma cor não saturada.
Se o centro de simetria for diferente de 0, pode ser definido com o
argumento vcenter . Para escala logarítmica em ambos os lados do centro, veja
colors.SymLogNormabaixo; para aplicar um mapeamento diferente acima e abaixo do centro, use colors.TwoSlopeNormabaixo.
delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2
# select a divergent colormap
cmap = cm.coolwarm
fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')
pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')
plt.show()
Logarítmico simétrico #
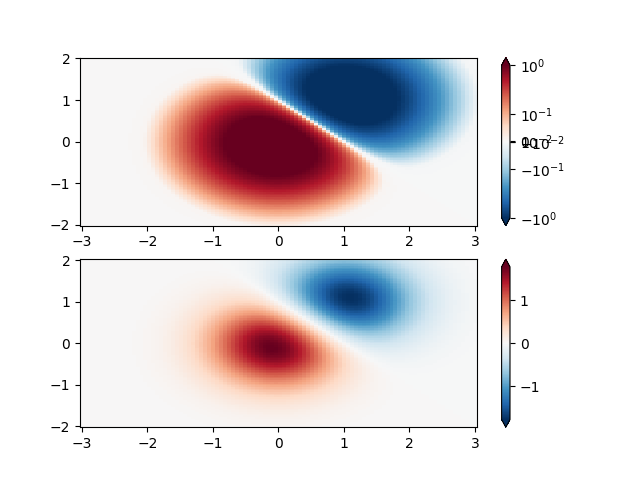
Da mesma forma, às vezes acontece que existem dados positivos e negativos, mas ainda assim gostaríamos que uma escala logarítmica fosse aplicada a ambos. Nesse caso, os números negativos também são escalados logaritmicamente e mapeados para números menores; por exemplo, se vmin=-vmax, então os números negativos são mapeados de 0 a 0,5 e os positivos de 0,5 a 1.
Como o logaritmo de valores próximos de zero tende para o infinito, uma pequena faixa em torno de zero precisa ser mapeada linearmente. O parâmetro linthresh permite ao usuário especificar o tamanho deste intervalo (- linthresh , linthresh ). O tamanho desse intervalo no mapa de cores é definido por linscale . Quando linscale == 1.0 (o padrão), o espaço usado para as metades positiva e negativa do intervalo linear será igual a uma década no intervalo logarítmico.
N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z,
norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
vmin=-1.0, vmax=1.0, base=10),
cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')
pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()
Lei de potência #
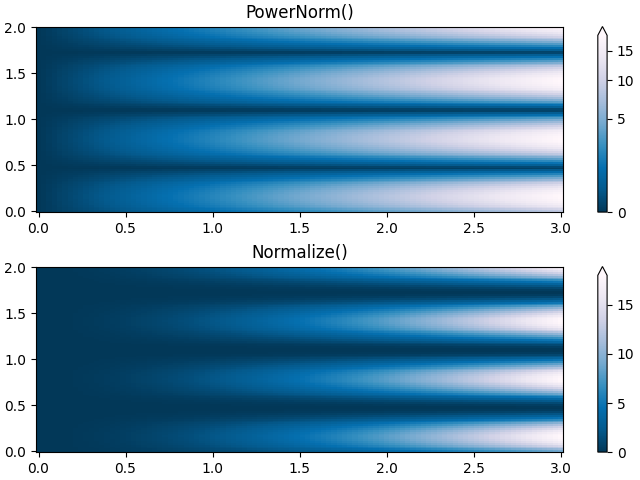
Às vezes é útil remapear as cores em uma relação de lei de potência (ou seja,\(y=x^{\gamma}\), Onde\(\gamma\)é o poder). Para isso utilizamos o colors.PowerNorm. Leva como argumento gamma ( gamma == 1.0 apenas produzirá a normalização linear padrão):
Observação
Provavelmente deve haver uma boa razão para plotar os dados usando esse tipo de transformação. Os visualizadores técnicos são usados para eixos lineares e logarítmicos e transformações de dados. As leis de poder são menos comuns e os espectadores devem ser explicitamente informados de que foram usadas.
N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots(2, 1, constrained_layout=True)
pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')
pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()
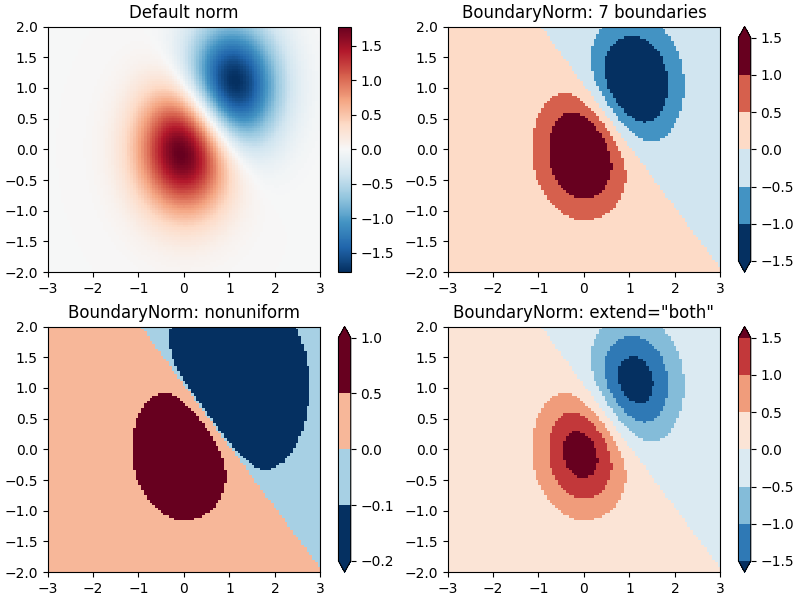
Limites discretos #
Outra normalização que vem com o Matplotlib é colors.BoundaryNorm. Além de vmin e vmax , isso toma como argumentos os limites entre os quais os dados devem ser mapeados. As cores são então distribuídas linearmente entre esses "limites". Também pode ser necessário um argumento estendido para adicionar valores superiores e/ou inferiores fora dos limites ao intervalo no qual as cores são distribuídas. Por exemplo:
Nota: Ao contrário das outras normas, esta norma retorna valores de 0 a ncolors -1.
N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]
fig, ax = plt.subplots(2, 2, figsize=(8, 6), constrained_layout=True)
ax = ax.flatten()
# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')
# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')
# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')
# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()
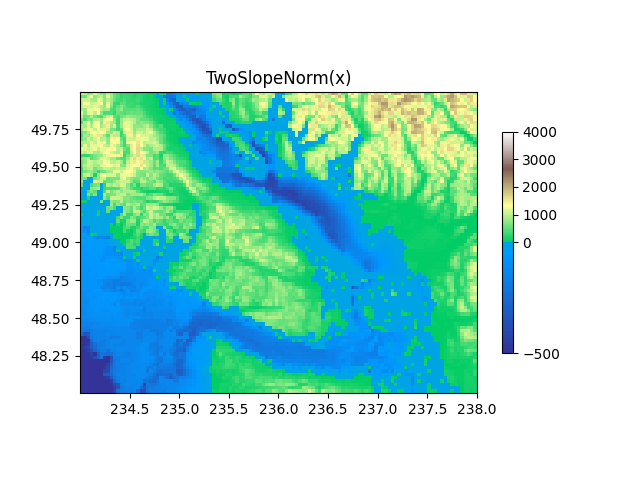
TwoSlopeNorm: Mapeamento diferente em ambos os lados de um centro #
Às vezes, queremos ter um mapa de cores diferente em cada lado de um ponto central conceitual e queremos que esses dois mapas de cores tenham escalas lineares diferentes. Um exemplo é um mapa topográfico em que a terra e o oceano têm um centro em zero, mas a terra normalmente tem uma faixa de elevação maior do que a profundidade da água, e geralmente são representados por um mapa de cores diferente.
dem = cbook.get_sample_data('topobathy.npz', np_load=True)
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']
fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
'terrain_map', all_colors)
# make the norm: Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)
pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()
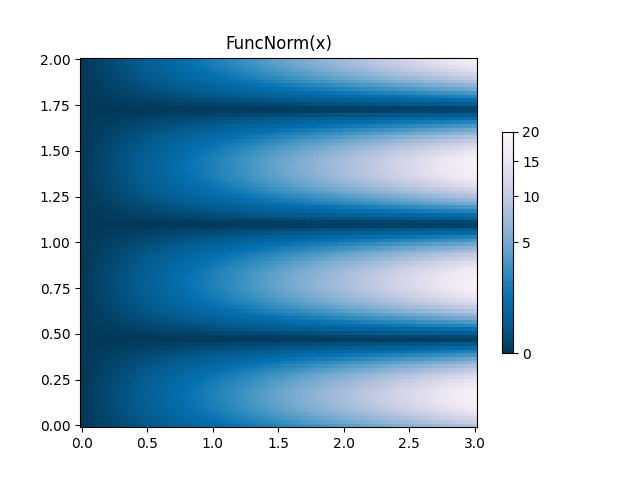
FuncNorm: Normalização de função arbitrária #
Se as normas acima não fornecem a normalização que você deseja, você pode usar
FuncNormpara definir a sua própria. Observe que este exemplo é o mesmo PowerNormcom uma potência de 0,5:
def _forward(x):
return np.sqrt(x)
def _inverse(x):
return x**2
N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()
norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()
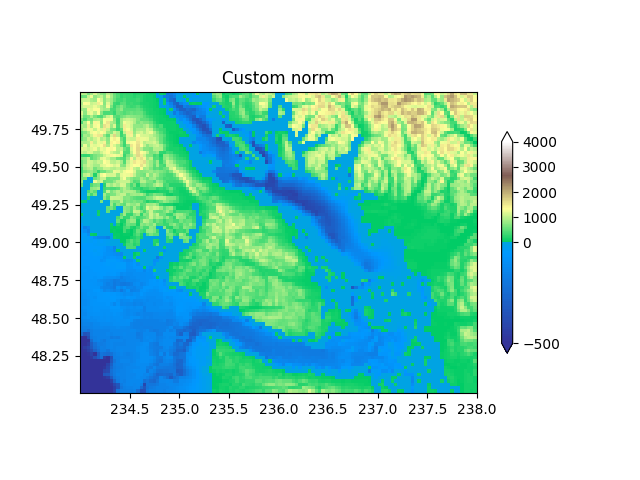
Normalização personalizada: implemente manualmente dois intervalos lineares #
O TwoSlopeNormdescrito acima é um exemplo útil para definir sua própria norma. Nota para que a barra de cores funcione, você deve definir um inverso para sua norma:
class MidpointNormalize(colors.Normalize):
def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
self.vcenter = vcenter
super().__init__(vmin, vmax, clip)
def __call__(self, value, clip=None):
# I'm ignoring masked values and all kinds of edge cases to make a
# simple example...
# Note also that we must extrapolate beyond vmin/vmax
x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
return np.ma.masked_array(np.interp(value, x, y,
left=-np.inf, right=np.inf))
def inverse(self, value):
y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
return np.interp(value, x, y, left=-np.inf, right=np.inf)
fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)
pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()
Tempo total de execução do script: ( 0 minutos 5,849 segundos)