Caminho Tutorial

Definindo caminhos em sua visualização do Matplotlib.

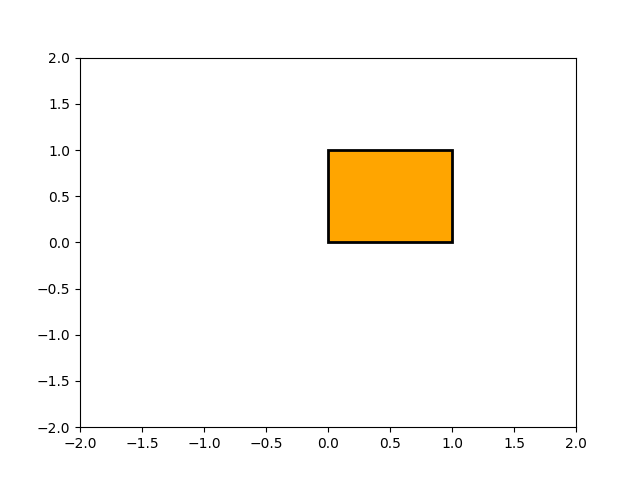
O objeto subjacente a todos os matplotlib.patchesobjetos é o Path, que suporta o conjunto padrão de comandos moveto, lineto, curveto para desenhar contornos simples e compostos que consistem em segmentos de linha e splines. O Pathé instanciado com uma matriz (N, 2) de (x, y) vértices e uma matriz de comprimento N de códigos de caminho. Por exemplo, para desenhar o retângulo unitário de (0, 0) a (1, 1), poderíamos usar este código:

import matplotlib.pyplot as plt
from matplotlib.path import Path
import matplotlib.patches as patches

verts = [
   (0., 0.),  # left, bottom
   (0., 1.),  # left, top
   (1., 1.),  # right, top
   (1., 0.),  # right, bottom
   (0., 0.),  # ignored
]

codes = [
    Path.MOVETO,
    Path.LINETO,
    Path.LINETO,
    Path.LINETO,
    Path.CLOSEPOLY,
]

path = Path(verts, codes)

fig, ax = plt.subplots()
patch = patches.PathPatch(path, facecolor='orange', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)
plt.show()

Os seguintes path codes são reconhecidos

Código	Vértices	Descrição
STOP	1 (ignorado)	Um marcador para o final de todo o caminho (atualmente não obrigatório e ignorado).
MOVETO	1	Pegue a caneta e mova para o vértice dado.
LINETO	1	Desenhe uma linha da posição atual até o vértice dado.
CURVE3	2: 1 ponto de controle, 1 ponto final	Desenhe uma curva Bézier quadrática da posição atual, com o ponto de controle dado, até o ponto final dado.
CURVE4	3: 2 pontos de controle, 1 ponto final	Desenhe uma curva cúbica de Bézier da posição atual, com os pontos de controle dados, até o ponto final dado.
CLOSEPOLY	1 (o ponto é ignorado)	Desenhe um segmento de linha até o ponto inicial da polilinha atual.

Bézier exemplo

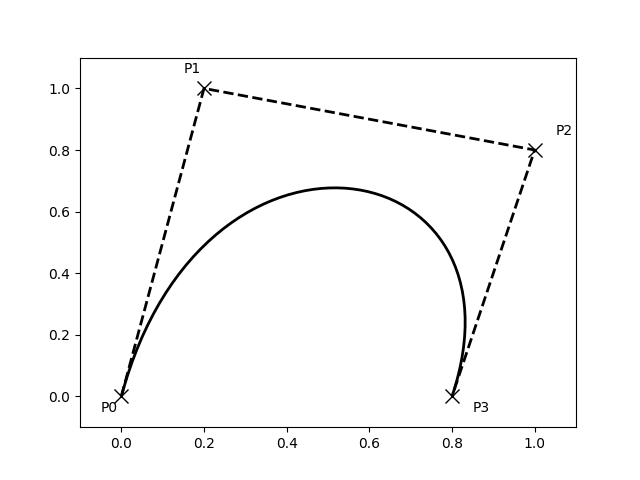
Alguns dos componentes do caminho requerem vários vértices para especificá-los: por exemplo, CURVE 3 é uma curva bézier com um ponto de controle e um ponto final, e CURVE4 tem três vértices para os dois pontos de controle e o ponto final. O exemplo abaixo mostra uma spline Bézier CURVE4 -- a curva Bézier estará contida na cobertura convexa do ponto inicial, os dois pontos de controle e o ponto final

verts = [
   (0., 0.),   # P0
   (0.2, 1.),  # P1
   (1., 0.8),  # P2
   (0.8, 0.),  # P3
]

codes = [
    Path.MOVETO,
    Path.CURVE4,
    Path.CURVE4,
    Path.CURVE4,
]

path = Path(verts, codes)

fig, ax = plt.subplots()
patch = patches.PathPatch(path, facecolor='none', lw=2)
ax.add_patch(patch)

xs, ys = zip(*verts)
ax.plot(xs, ys, 'x--', lw=2, color='black', ms=10)

ax.text(-0.05, -0.05, 'P0')
ax.text(0.15, 1.05, 'P1')
ax.text(1.05, 0.85, 'P2')
ax.text(0.85, -0.05, 'P3')

ax.set_xlim(-0.1, 1.1)
ax.set_ylim(-0.1, 1.1)
plt.show()

Caminhos compostos

Todas as primitivas de patch simples em matplotlib, retângulo, círculo, polígono, etc, são implementadas com caminho simples. Funções de plotagem como hist()e bar(), que criam vários primitivos, por exemplo, um monte de retângulos, geralmente podem ser implementadas com mais eficiência usando um caminho composto. A razão para barcriar uma lista de retângulos e não um caminho composto é amplamente histórica: o Pathcódigo é comparativamente novo e bar é anterior a ele. Embora pudéssemos alterá-lo agora, isso quebraria o código antigo; portanto, abordaremos aqui como criar caminhos compostos, substituindo a funcionalidade na barra, caso você precise fazer isso em seu próprio código por motivos de eficiência, por exemplo, você está criando um gráfico de barras animado.

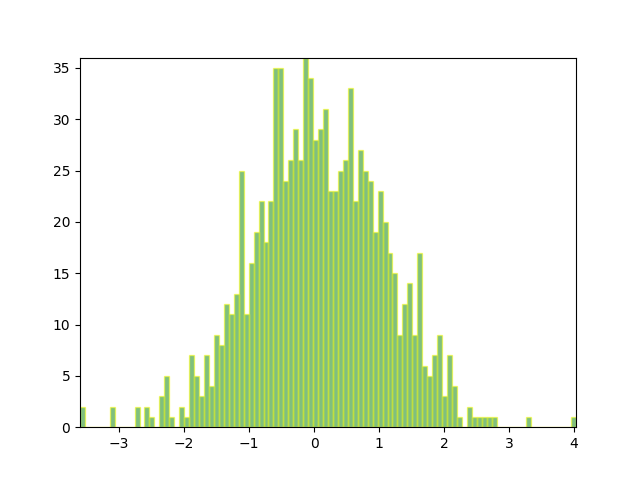
Faremos o gráfico de histograma criando uma série de retângulos para cada barra de histograma: a largura do retângulo é a largura do compartimento e a altura do retângulo é o número de pontos de dados nesse compartimento. Primeiro, criaremos alguns dados aleatórios normalmente distribuídos e calcularemos o histograma. Como numpy retorna as bordas do compartimento e não os centros, o comprimento de binsé 1 maior que o comprimento de nno exemplo abaixo:

# histogram our data with numpy
data = np.random.randn(1000)
n, bins = np.histogram(data, 100)

Agora vamos extrair os cantos dos retângulos. Cada uma das matrizes left, bottom, etc, abaixo é len(n), onde né a matriz de contagens para cada barra do histograma:

# get the corners of the rectangles for the histogram
left = np.array(bins[:-1])
right = np.array(bins[1:])
bottom = np.zeros(len(left))
top = bottom + n

Agora temos que construir nosso caminho composto, que consistirá em uma série de MOVETO, LINETOe CLOSEPOLYpara cada retângulo. Para cada retângulo, precisamos de 5 vértices: 1 para o MOVETO, 3 para o LINETOe 1 para o CLOSEPOLY. Conforme indicado na tabela acima, o vértice para o closepoly é ignorado, mas ainda precisamos dele para manter os códigos alinhados com os vértices:

nverts = nrects*(1+3+1)
verts = np.zeros((nverts, 2))
codes = np.ones(nverts, int) * path.Path.LINETO
codes[0::5] = path.Path.MOVETO
codes[4::5] = path.Path.CLOSEPOLY
verts[0::5, 0] = left
verts[0::5, 1] = bottom
verts[1::5, 0] = left
verts[1::5, 1] = top
verts[2::5, 0] = right
verts[2::5, 1] = top
verts[3::5, 0] = right
verts[3::5, 1] = bottom

Tudo o que resta é criar o caminho, anexá-lo a um PathPatche adicioná-lo aos nossos eixos:

barpath = path.Path(verts, codes)
patch = patches.PathPatch(barpath, facecolor='green',
  edgecolor='yellow', alpha=0.5)
ax.add_patch(patch)

import numpy as np
import matplotlib.patches as patches
import matplotlib.path as path

fig, ax = plt.subplots()
# Fixing random state for reproducibility
np.random.seed(19680801)

# histogram our data with numpy
data = np.random.randn(1000)
n, bins = np.histogram(data, 100)

# get the corners of the rectangles for the histogram
left = np.array(bins[:-1])
right = np.array(bins[1:])
bottom = np.zeros(len(left))
top = bottom + n
nrects = len(left)

nverts = nrects*(1+3+1)
verts = np.zeros((nverts, 2))
codes = np.ones(nverts, int) * path.Path.LINETO
codes[0::5] = path.Path.MOVETO
codes[4::5] = path.Path.CLOSEPOLY
verts[0::5, 0] = left
verts[0::5, 1] = bottom
verts[1::5, 0] = left
verts[1::5, 1] = top
verts[2::5, 0] = right
verts[2::5, 1] = top
verts[3::5, 0] = right
verts[3::5, 1] = bottom

barpath = path.Path(verts, codes)
patch = patches.PathPatch(barpath, facecolor='green',
                          edgecolor='yellow', alpha=0.5)
ax.add_patch(patch)

ax.set_xlim(left[0], right[-1])
ax.set_ylim(bottom.min(), top.max())

plt.show()