Tutorial de Transformações

Como qualquer pacote gráfico, o Matplotlib é construído sobre uma estrutura de transformação para mover-se facilmente entre os sistemas de coordenadas, o sistema de coordenadas de dados da área do usuário, o sistema de coordenadas de eixos , o sistema de coordenadas de figuras e o sistema de coordenadas de exibição . Em 95% da sua plotagem, você não precisará pensar sobre isso, como acontece nos bastidores, mas conforme você ultrapassa os limites da geração de figuras personalizadas, é útil ter uma compreensão desses objetos para que você possa reutilizar os existentes transformações que o Matplotlib disponibiliza para você ou crie as suas próprias (consulte Recursos matplotlib.transforms). A tabela abaixo resume alguns sistemas de coordenadas úteis, uma descrição de cada sistema e o objeto de transformação para ir de cada sistema de coordenadas para oexibir coordenadas. Na coluna "Objeto de transformação", axé uma Axesinstância, figé uma Figureinstância e subfigureé uma SubFigureinstância.

Sistema de coordenadas	Descrição	Objeto de transformação do sistema para exibição
"dados"	O sistema de coordenadas dos dados nos Axes.	ax.transData
"machados"	O sistema de coordenadas do Axes; (0, 0) é o canto inferior esquerdo dos eixos e (1, 1) é o canto superior direito dos eixos.	ax.transAxes
"subfigura"	O sistema de coordenadas do SubFigure; (0, 0) é o canto inferior esquerdo da subfigura e (1, 1) é o canto superior direito da subfigura. Se uma figura não tiver subfiguras, isso é o mesmo que transFigure.	subfigure.transSubfigure
"figura"	O sistema de coordenadas do Figure; (0, 0) é o canto inferior esquerdo da figura e (1, 1) é o canto superior direito da figura.	fig.transFigure
"figura-polegadas"	O sistema de coordenadas Figureem polegadas; (0, 0) é o canto inferior esquerdo da figura e (largura, altura) é o canto superior direito da figura em polegadas.	fig.dpi_scale_trans
"xaxis", "yaxis"	Sistemas de coordenadas combinadas, usando coordenadas de dados em uma direção e coordenadas de eixos na outra.	ax.get_xaxis_transform(), ax.get_yaxis_transform()
"exibição"	O sistema de coordenadas nativo da saída; (0, 0) é a parte inferior esquerda da janela e (largura, altura) é a parte superior direita da saída em "unidades de exibição". A interpretação exata das unidades depende do back-end. Por exemplo, são pixels para Agg e pontos para svg/pdf.	None, ou IdentityTransform()

Os Transformobjetos são ingênuos aos sistemas de coordenadas de origem e destino, no entanto, os objetos referidos na tabela acima são construídos para receber entradas em seu sistema de coordenadas e transformar a entrada no sistema de coordenadas de exibição . É por isso que o sistema de coordenadas de exibiçãoNone tem para a coluna "Objeto de transformação" -- ele já está em coordenadas de exibição . As convenções de nomenclatura e destino são uma ajuda para acompanhar os sistemas de coordenadas "padrão" disponíveis e as transformações.

As transformações também sabem como se inverter (via Transform.inverted) para gerar uma transformação do sistema de coordenadas de saída de volta para o sistema de coordenadas de entrada. Por exemplo, ax.transDataconverte valores em coordenadas de dados em coordenadas de exibição e ax.transData.inversed()é um matplotlib.transforms.Transformque vai de coordenadas de exibição em coordenadas de dados. Isso é particularmente útil ao processar eventos da interface do usuário, que normalmente ocorrem no espaço de exibição, e você deseja saber onde o clique do mouse ou o pressionamento de tecla ocorreu em seu sistema de coordenadas de dados .

Observe que especificar a posição dos artistas nas coordenadas de exibiçãodpi pode alterar sua localização relativa se o tamanho ou o tamanho da figura mudar. Isso pode causar confusão ao imprimir ou alterar a resolução da tela, porque o objeto pode mudar de local e tamanho. Portanto, é mais comum que artistas colocados em um eixo ou figura tenham sua transformação definida para algo diferente de IdentityTransform(); o padrão quando um artista é adicionado a um Axes usando add_artisté que a transformação seja ax.transDatapara que você possa trabalhar e pensar em coordenadas de dados e deixar que o Matplotlib cuide da transformação a ser exibida .

Coordenadas de dados

Vamos começar com a coordenada mais comumente usada, o sistema de coordenadas de dados . Sempre que você adiciona dados aos eixos, o Matplotlib atualiza os limites de dados, mais comumente atualizados com os métodos set_xlim()e . set_ylim()Por exemplo, na figura abaixo, os limites de dados variam de 0 a 10 no eixo x e -1 a 1 no eixo y.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

plt.show()

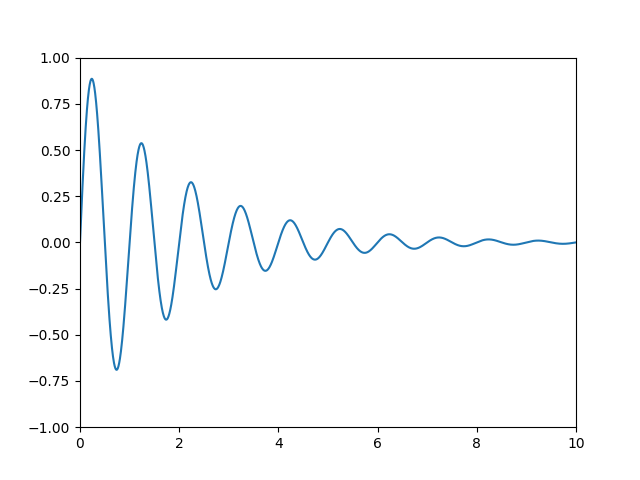
Você pode usar a ax.transDatainstância para transformar seus dados em seu sistema de coordenadas de exibição , seja um único ponto ou uma sequência de pontos, conforme mostrado abaixo:

In [14]: type(ax.transData)
Out[14]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [15]: ax.transData.transform((5, 0))
Out[15]: array([ 335.175,  247.   ])

In [16]: ax.transData.transform([(5, 0), (1, 2)])
Out[16]:
array([[ 335.175,  247.   ],
       [ 132.435,  642.2  ]])

Você pode usar o inverted() método para criar uma transformação que o levará da exibição para as coordenadas de dados :

In [41]: inv = ax.transData.inverted()

In [42]: type(inv)
Out[42]: <class 'matplotlib.transforms.CompositeGenericTransform'>

In [43]: inv.transform((335.175,  247.))
Out[43]: array([ 5.,  0.])

Se você estiver digitando junto com este tutorial, os valores exatos das coordenadas de exibição podem diferir se você tiver um tamanho de janela ou configuração de dpi diferente. Da mesma forma, na figura abaixo, os pontos rotulados de exibição provavelmente não são os mesmos da sessão do ipython porque os padrões de tamanho da figura da documentação são diferentes.

x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)

xdata, ydata = 5, 0
# This computing the transform now, if anything
# (figure size, dpi, axes placement, data limits, scales..)
# changes re-calling transform will get a different value.
xdisplay, ydisplay = ax.transData.transform((xdata, ydata))

bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
    arrowstyle="->",
    connectionstyle="angle,angleA=0,angleB=90,rad=10")

offset = 72
ax.annotate('data = (%.1f, %.1f)' % (xdata, ydata),
            (xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
            bbox=bbox, arrowprops=arrowprops)

disp = ax.annotate('display = (%.1f, %.1f)' % (xdisplay, ydisplay),
                   (xdisplay, ydisplay), xytext=(0.5*offset, -offset),
                   xycoords='figure pixels',
                   textcoords='offset points',
                   bbox=bbox, arrowprops=arrowprops)

plt.show()

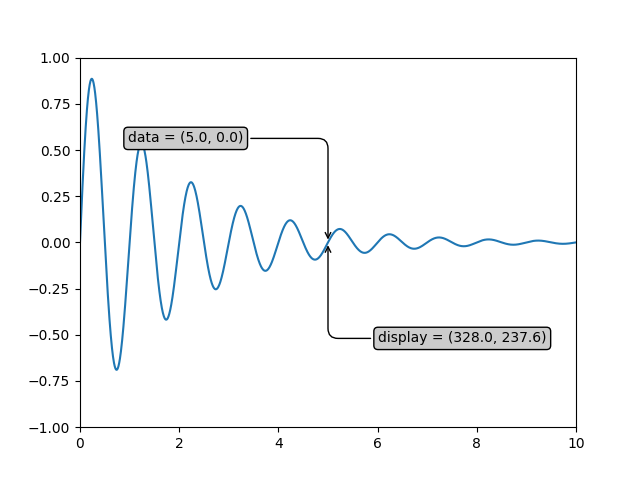
Aviso

Se você executar o código-fonte no exemplo acima em um back-end de GUI, também poderá descobrir que as duas setas para as anotações de dados e exibição não apontam exatamente para o mesmo ponto. Isso ocorre porque o ponto de exibição foi calculado antes de a figura ser exibida, e o back-end da GUI pode redimensionar ligeiramente a figura quando ela é criada. O efeito é mais pronunciado se você mesmo redimensionar a figura. Este é um bom motivo pelo qual você raramente deseja trabalhar no espaço de exibição , mas pode se conectar ao 'on_draw' Eventpara atualizar as coordenadas da figura nos desenhos da figura; consulte Manipulação e seleção de eventos .

Quando você altera os limites x ou y de seus eixos, os limites de dados são atualizados para que a transformação produza um novo ponto de exibição. Note que quando mudamos apenas o ylim, apenas a coordenada de exibição y é alterada, e quando mudamos o xlim também, ambos são alterados. Mais sobre isso mais tarde, quando falarmos sobre o Bbox.

In [54]: ax.transData.transform((5, 0))
Out[54]: array([ 335.175,  247.   ])

In [55]: ax.set_ylim(-1, 2)
Out[55]: (-1, 2)

In [56]: ax.transData.transform((5, 0))
Out[56]: array([ 335.175     ,  181.13333333])

In [57]: ax.set_xlim(10, 20)
Out[57]: (10, 20)

In [58]: ax.transData.transform((5, 0))
Out[58]: array([-171.675     ,  181.13333333])

Coordenadas dos eixos

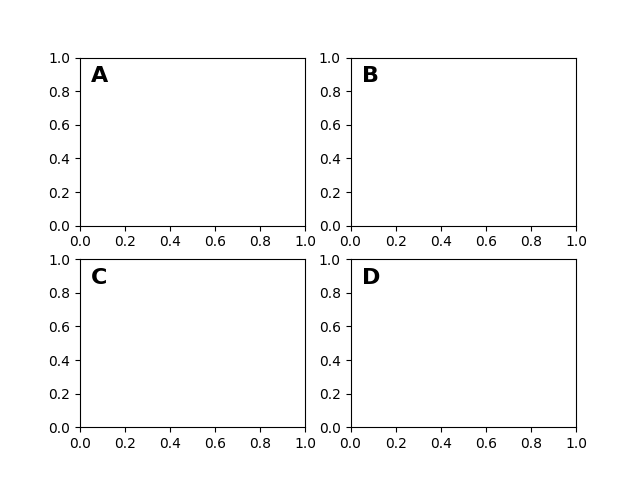
Depois do sistema de coordenadas de dados , os eixos são provavelmente o segundo sistema de coordenadas mais útil. Aqui, o ponto (0, 0) é o canto inferior esquerdo de seus eixos ou subplot, (0,5, 0,5) é o centro e (1,0, 1,0) é o canto superior direito. Você também pode se referir a pontos fora do intervalo, então (-0,1, 1,1) está à esquerda e acima de seus eixos. Este sistema de coordenadas é extremamente útil ao colocar texto em seus eixos, porque muitas vezes você deseja uma bolha de texto em um local fixo, por exemplo, no canto superior esquerdo do painel de eixos, e manter esse local fixo quando você deslocar ou aplicar zoom. Aqui está um exemplo simples que cria quatro painéis e os rotula 'A', 'B', 'C', 'D' como você costuma ver em diários.

fig = plt.figure()
for i, label in enumerate(('A', 'B', 'C', 'D')):
    ax = fig.add_subplot(2, 2, i+1)
    ax.text(0.05, 0.95, label, transform=ax.transAxes,
            fontsize=16, fontweight='bold', va='top')

plt.show()

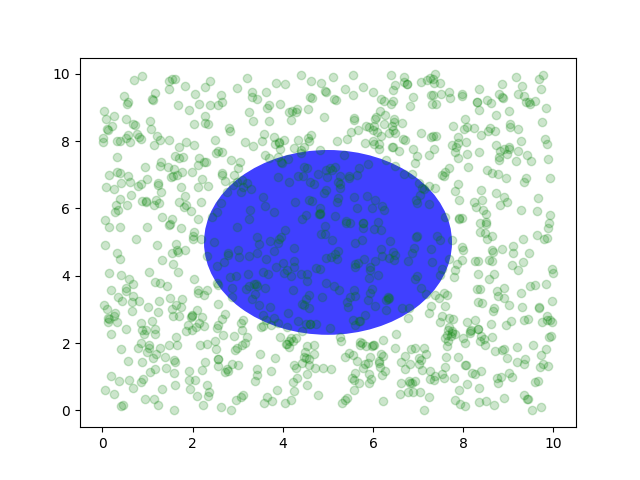
Você também pode fazer linhas ou patches no sistema de coordenadas de eixos , mas isso é menos útil na minha experiência do que usar ax.transAxespara colocar texto. No entanto, aqui está um exemplo bobo que plota alguns pontos aleatórios no espaço de dados e sobrepõe um semitransparente Circlecentralizado no meio dos eixos com um raio de um quarto dos eixos - se seus eixos não preservarem a proporção (consulte set_aspect()) , isso se parecerá com uma elipse. Use a ferramenta pan/zoom para mover, ou altere manualmente os dados xlim e ylim, e você verá os dados se moverem, mas o círculo permanecerá fixo porque não está nas coordenadas de dados e sempre permanecerá no centro dos eixos .

fig, ax = plt.subplots()
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y, 'go', alpha=0.2)  # plot some data in data coordinates

circ = mpatches.Circle((0.5, 0.5), 0.25, transform=ax.transAxes,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Transformações combinadas

Desenhar em espaços de coordenadas combinadas que misturam eixos com coordenadas de dados é extremamente útil, por exemplo, para criar uma extensão horizontal que destaca alguma região dos dados y, mas abrange o eixo x, independentemente dos limites de dados, pan ou nível de zoom, etc. Na verdade, essas linhas e extensões combinadas são tão úteis que construímos funções para torná-las fáceis de plotar (consulte axhline(), axvline(), axhspan(), axvspan()), mas, para fins didáticos, implementaremos a extensão horizontal aqui usando uma transformação combinada. Este truque funciona apenas para transformações separáveis, como você vê em sistemas de coordenadas cartesianas normais, mas não em transformações inseparáveis ​​como o PolarTransform.

import matplotlib.transforms as transforms

fig, ax = plt.subplots()
x = np.random.randn(1000)

ax.hist(x, 30)
ax.set_title(r'$\sigma=1 \/ \dots \/ \sigma=2$', fontsize=16)

# the x coords of this transformation are data, and the y coord are axes
trans = transforms.blended_transform_factory(
    ax.transData, ax.transAxes)
# highlight the 1..2 stddev region with a span.
# We want x to be in data coordinates and y to span from 0..1 in axes coords.
rect = mpatches.Rectangle((1, 0), width=1, height=1, transform=trans,
                          color='yellow', alpha=0.5)
ax.add_patch(rect)

plt.show()

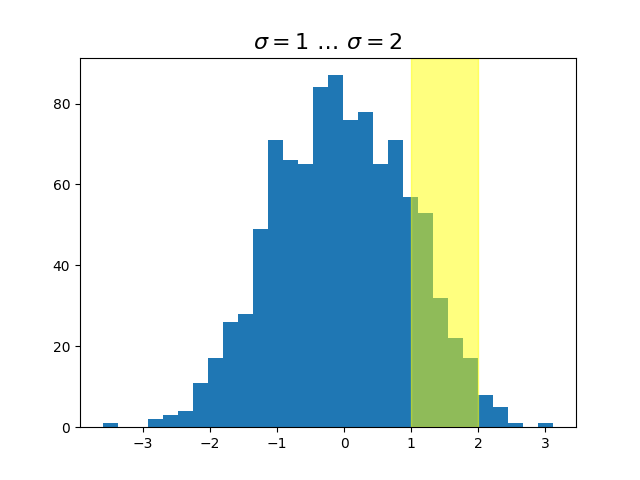
Observação

As transformações combinadas onde x está em coordenadas de dados e y em coordenadas de eixos são tão úteis que temos métodos auxiliares para retornar as versões que o Matplotlib usa internamente para desenhar ticks, ticklabels, etc. Os métodos são matplotlib.axes.Axes.get_xaxis_transform()e matplotlib.axes.Axes.get_yaxis_transform(). Portanto, no exemplo acima, a chamada para blended_transform_factory()pode ser substituída por get_xaxis_transform:

trans = ax.get_xaxis_transform()

Plotando em coordenadas físicas

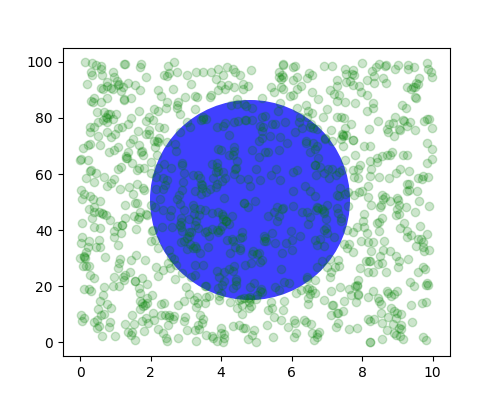
Às vezes, queremos que um objeto tenha um determinado tamanho físico no gráfico. Aqui desenhamos o mesmo círculo acima, mas em coordenadas físicas. Se feito de forma interativa, você pode ver que alterar o tamanho da figura não altera o deslocamento do círculo do canto inferior esquerdo, não altera seu tamanho e o círculo permanece um círculo, independentemente da proporção dos eixos.

fig, ax = plt.subplots(figsize=(5, 4))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

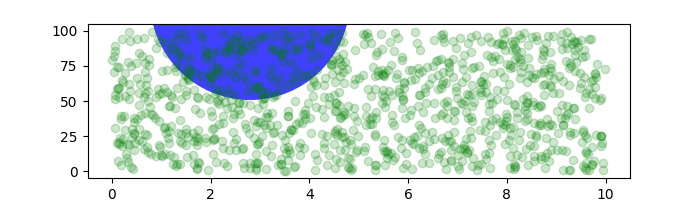
Se mudarmos o tamanho da figura, o círculo não muda sua posição absoluta e é recortado.

fig, ax = plt.subplots(figsize=(7, 2))
x, y = 10*np.random.rand(2, 1000)
ax.plot(x, y*10., 'go', alpha=0.2)  # plot some data in data coordinates
# add a circle in fixed-coordinates
circ = mpatches.Circle((2.5, 2), 1.0, transform=fig.dpi_scale_trans,
                       facecolor='blue', alpha=0.75)
ax.add_patch(circ)
plt.show()

Outro uso é colocar um patch com uma dimensão física definida em torno de um ponto de dados nos eixos. Aqui somamos duas transformações. O primeiro define a escala de quão grande a elipse deve ser e o segundo define sua posição. A elipse é então colocada na origem e então usamos a transformação auxiliar ScaledTranslation para movê-la para o lugar certo no ax.transDatasistema de coordenadas. Este auxiliar é instanciado com:

trans = ScaledTranslation(xt, yt, scale_trans)

onde xt e yt são os deslocamentos de translação e scale_trans é uma transformação que dimensiona xt e yt no tempo de transformação antes de aplicar os deslocamentos.

Observe o uso do operador de adição nas transformações abaixo. Este código diz: primeiro aplique a transformação de escala fig.dpi_scale_trans para tornar a elipse do tamanho adequado, mas ainda centralizada em (0, 0) e, em seguida, transfira os dados para xdata[0]e ydata[0]no espaço de dados.

No uso interativo, a elipse permanece do mesmo tamanho mesmo que os limites dos eixos sejam alterados via zoom.

fig, ax = plt.subplots()
xdata, ydata = (0.2, 0.7), (0.5, 0.5)
ax.plot(xdata, ydata, "o")
ax.set_xlim((0, 1))

trans = (fig.dpi_scale_trans +
         transforms.ScaledTranslation(xdata[0], ydata[0], ax.transData))

# plot an ellipse around the point that is 150 x 130 points in diameter...
circle = mpatches.Ellipse((0, 0), 150/72, 130/72, angle=40,
                          fill=None, transform=trans)
ax.add_patch(circle)
plt.show()

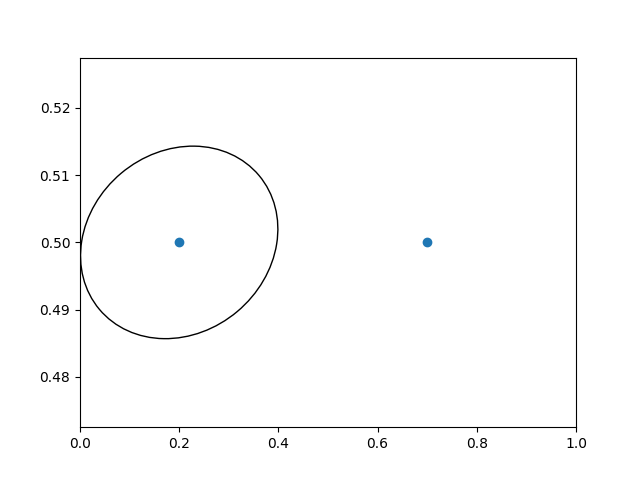
Observação

A ordem da transformação é importante. Aqui, a elipse recebe primeiro as dimensões corretas no espaço de exibição e, em seguida, é movida no espaço de dados para o local correto. Se tivéssemos feito o ScaledTranslationprimeiro, então xdata[0]e ydata[0]seria primeiro transformado para exibir coordenadas ( em um monitor de 200 dpi) e então essas coordenadas seriam dimensionadas empurrando o centro da elipse bem para fora da tela (ou seja, ).[ 358.4  475.2]fig.dpi_scale_trans[ 71680.  95040.]

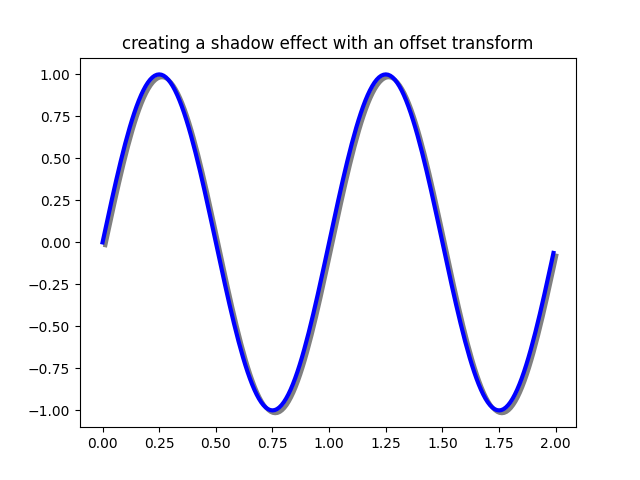
Usando transformações de deslocamento para criar um efeito de sombra

Outro uso de ScaledTranslationé criar uma nova transformação que é deslocada de outra transformação, por exemplo, para colocar um objeto deslocado um pouco em relação a outro objeto. Normalmente, você deseja que o deslocamento esteja em alguma dimensão física, como pontos ou polegadas, em vez de coordenadas de dados , para que o efeito do deslocamento seja constante em diferentes níveis de zoom e configurações de dpi.

Um uso para um deslocamento é criar um efeito de sombra, onde você desenha um objeto idêntico ao primeiro logo à direita dele e logo abaixo dele, ajustando a zorder para garantir que a sombra seja desenhada primeiro e depois o objeto que é sombreando acima dela.

Aqui aplicamos as transformações na ordem oposta ao uso ScaledTranslationacima. O gráfico é feito primeiro em coordenadas de dados ( ax.transData) e depois deslocado por dxe dypontos usando fig.dpi_scale_trans. (Na tipografia, um ponto é 1/72 polegadas e, ao especificar seus deslocamentos em pontos, sua figura terá a mesma aparência, independentemente da resolução dpi em que foi salva.)

fig, ax = plt.subplots()

# make a simple sine wave
x = np.arange(0., 2., 0.01)
y = np.sin(2*np.pi*x)
line, = ax.plot(x, y, lw=3, color='blue')

# shift the object over 2 points, and down 2 points
dx, dy = 2/72., -2/72.
offset = transforms.ScaledTranslation(dx, dy, fig.dpi_scale_trans)
shadow_transform = ax.transData + offset

# now plot the same data with our offset transform;
# use the zorder to make sure we are below the line
ax.plot(x, y, lw=3, color='gray',
        transform=shadow_transform,
        zorder=0.5*line.get_zorder())

ax.set_title('creating a shadow effect with an offset transform')
plt.show()

Observação

O deslocamento de dpi e polegadas é um caso de uso tão comum que temos uma função auxiliar especial para criá-lo matplotlib.transforms.offset_copy(), que retorna uma nova transformação com um deslocamento adicionado. Então acima poderíamos ter feito:

shadow_transform = transforms.offset_copy(ax.transData,
         fig=fig, dx, dy, units='inches')

O pipeline de transformação

A ax.transDatatransformação com a qual trabalhamos neste tutorial é uma composição de três transformações diferentes que compõem o pipeline de transformação de dados -> exibição coordenadas. Michael Droettboom implementou a estrutura de transformações, tendo o cuidado de fornecer uma API limpa que segregou as projeções e escalas não lineares que ocorrem em plotagens polares e logarítmicas, das transformações lineares afins que ocorrem quando você desloca e aplica zoom. Há uma eficiência aqui, porque você pode aplicar pan e zoom em seus eixos, o que afeta a transformação afim, mas talvez não seja necessário calcular as escalas ou projeções não lineares potencialmente caras em eventos de navegação simples. Também é possível multiplicar matrizes de transformação afim juntas e aplicá-las às coordenadas em uma única etapa. Isso não é verdade para todas as transformações possíveis.

Aqui está como a ax.transDatainstância é definida na classe básica de eixo separável Axes:

self.transData = self.transScale + (self.transLimits + self.transAxes)

Fomos apresentados à transAxesinstância acima em Coordenadas de eixos , que mapeia os cantos (0, 0), (1, 1) dos eixos ou caixa delimitadora de subtrama para exibir o espaço, então vamos ver essas outras duas partes.

self.transLimitsé a transformação que leva você dos dados às coordenadas dos eixos ; ou seja, ele mapeia sua visão xlim e ylim para o espaço unitário dos eixos (e transAxesentão leva esse espaço unitário para exibir o espaço). Podemos ver isso em ação aqui

In [80]: ax = plt.subplot()

In [81]: ax.set_xlim(0, 10)
Out[81]: (0, 10)

In [82]: ax.set_ylim(-1, 1)
Out[82]: (-1, 1)

In [84]: ax.transLimits.transform((0, -1))
Out[84]: array([ 0.,  0.])

In [85]: ax.transLimits.transform((10, -1))
Out[85]: array([ 1.,  0.])

In [86]: ax.transLimits.transform((10, 1))
Out[86]: array([ 1.,  1.])

In [87]: ax.transLimits.transform((5, 0))
Out[87]: array([ 0.5,  0.5])

e podemos usar essa mesma transformação invertida para voltar das coordenadas dos eixos unitários às coordenadas dos dados .

In [90]: inv.transform((0.25, 0.25))
Out[90]: array([ 2.5, -0.5])

A peça final é o self.transScaleatributo, que é responsável pela escala opcional não linear dos dados, por exemplo, para eixos logarítmicos. Quando um Axes é configurado inicialmente, isso é definido apenas para a transformação de identidade, já que os eixos básicos do Matplotlib têm escala linear, mas quando você chama uma função de escala logarítmica como semilogx()ou define explicitamente a escala como logarítmica com set_xscale(), o ax.transScaleatributo é definido para manipular a projeção não linear. As transformações de escalas são propriedades das respectivas instâncias xaxise . yaxis AxisPor exemplo, quando você chama ax.set_xscale('log'), o xaxis atualiza sua escala para uma matplotlib.scale.LogScaleinstância.

Para eixos não separáveis, os PolarAxes, há mais uma peça a considerar, a transformação da projeção. O transData matplotlib.projections.polar.PolarAxesé semelhante ao dos típicos eixos matplotlib separáveis, com uma peça adicional transProjection:

self.transData = self.transScale + self.transProjection + \
    (self.transProjectionAffine + self.transAxes)

transProjectionmanipula a projeção do espaço, por exemplo, latitude e longitude para dados de mapa, ou raio e teta para dados polares, para um sistema de coordenadas cartesiano separável. Existem vários exemplos de projeção no matplotlib.projectionspacote, e a melhor maneira de aprender mais é abrir o código-fonte desses pacotes e ver como fazer o seu próprio, já que o Matplotlib suporta eixos e projeções extensíveis. Michael Droettboom forneceu um bom exemplo de tutorial para criar eixos de projeção Hammer; consulte Projeção personalizada .