Observação
Clique aqui para baixar o código de exemplo completo
Tutorial de imagem #
Um breve tutorial sobre plotagem de imagens com Matplotlib.
Comandos de inicialização #
Primeiro, vamos iniciar o IPython. É um aprimoramento excelente para o prompt padrão do Python e se relaciona especialmente bem com o Matplotlib. Inicie o IPython diretamente em um shell ou com o Jupyter Notebook (onde o IPython é um kernel em execução).
Com o IPython iniciado, agora precisamos nos conectar a um loop de eventos da GUI. Isso diz ao IPython onde (e como) exibir gráficos. Para se conectar a um loop de GUI, execute a mágica %matplotlib no prompt do IPython. Há mais detalhes sobre exatamente o que isso faz na documentação do IPython sobre loops de eventos da GUI .
Se você estiver usando o Jupyter Notebook, os mesmos comandos estarão disponíveis, mas as pessoas geralmente usam um argumento específico para a mágica %matplotlib:
In [1]: %matplotlib inline
Isso ativa a plotagem em linha, onde os gráficos de plotagem aparecerão em seu notebook. Isso tem implicações importantes para a interatividade. Para plotagem em linha, os comandos nas células abaixo da célula que gera uma plotagem não afetarão a plotagem. Por exemplo, não é possível alterar o mapa de cores nas células abaixo da célula que cria um gráfico. No entanto, para outros backends, como o Qt, que abrem uma janela separada, as células abaixo daquelas que criam o gráfico irão alterar o gráfico - é um objeto vivo na memória.
Este tutorial usará a interface de plotagem implícita do Matplotlib, pyplot. Essa interface mantém o estado global e é muito útil para experimentar rápida e facilmente várias configurações de plotagem. A alternativa é a explícita, que é mais adequada para o desenvolvimento de grandes aplicações. Para obter uma explicação das compensações entre as interfaces implícita e explícita, consulte Matplotlib Application Interfaces (APIs) e o guia de início rápido para começar a usar a interface explícita. Por enquanto, vamos continuar com a abordagem implícita:
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
Importando dados de imagem para matrizes Numpy #
Matplotlib depende da biblioteca Pillow para carregar dados de imagem.
Aqui está a imagem com a qual vamos jogar:

É uma imagem PNG RGB de 24 bits (8 bits para cada R, G, B). Dependendo de onde você obtém seus dados, os outros tipos de imagem que você provavelmente encontrará são imagens RGBA, que permitem transparência, ou imagens em escala de cinza (luminosidade) de canal único. Baixe stinkbug.png para o seu computador para o restante deste tutorial.
E aqui vamos nós...
img = mpimg.imread('../../doc/_static/stinkbug.png')
print(img)
[[[0.40784314 0.40784314 0.40784314]
[0.40784314 0.40784314 0.40784314]
[0.40784314 0.40784314 0.40784314]
...
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]]
[[0.4117647 0.4117647 0.4117647 ]
[0.4117647 0.4117647 0.4117647 ]
[0.4117647 0.4117647 0.4117647 ]
...
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]
[0.42745098 0.42745098 0.42745098]]
[[0.41960785 0.41960785 0.41960785]
[0.41568628 0.41568628 0.41568628]
[0.41568628 0.41568628 0.41568628]
...
[0.43137255 0.43137255 0.43137255]
[0.43137255 0.43137255 0.43137255]
[0.43137255 0.43137255 0.43137255]]
...
[[0.4392157 0.4392157 0.4392157 ]
[0.43529412 0.43529412 0.43529412]
[0.43137255 0.43137255 0.43137255]
...
[0.45490196 0.45490196 0.45490196]
[0.4509804 0.4509804 0.4509804 ]
[0.4509804 0.4509804 0.4509804 ]]
[[0.44313726 0.44313726 0.44313726]
[0.44313726 0.44313726 0.44313726]
[0.4392157 0.4392157 0.4392157 ]
...
[0.4509804 0.4509804 0.4509804 ]
[0.44705883 0.44705883 0.44705883]
[0.44705883 0.44705883 0.44705883]]
[[0.44313726 0.44313726 0.44313726]
[0.4509804 0.4509804 0.4509804 ]
[0.4509804 0.4509804 0.4509804 ]
...
[0.44705883 0.44705883 0.44705883]
[0.44705883 0.44705883 0.44705883]
[0.44313726 0.44313726 0.44313726]]]
Observe o dtype lá - float32. Matplotlib redimensionou os dados de 8 bits de cada canal para dados de ponto flutuante entre 0,0 e 1,0. Como observação, o único tipo de dados com o qual o Pillow pode trabalhar é uint8. A plotagem Matplotlib pode lidar com float32 e uint8, mas a leitura/gravação de imagem para qualquer formato diferente de PNG é limitada a dados uint8. Por que 8 bits? A maioria dos monitores pode renderizar apenas 8 bits por canal de gradação de cores. Por que eles só podem renderizar 8 bits/canal? Porque isso é tudo que o olho humano pode ver. Mais aqui (do ponto de vista da fotografia): Luminous Landscape bit depth tutorial .
Cada lista interna representa um pixel. Aqui, com uma imagem RGB, existem 3 valores. Como é uma imagem em preto e branco, R, G e B são todos semelhantes. Um RGBA (onde A é alfa ou transparência) tem 4 valores por lista interna e uma imagem de luminância simples tem apenas um valor (e, portanto, é apenas uma matriz 2-D, não uma matriz 3-D). Para imagens RGB e RGBA, o Matplotlib oferece suporte aos tipos de dados float32 e uint8. Para tons de cinza, o Matplotlib suporta apenas float32. Se os dados da sua matriz não atenderem a uma dessas descrições, você precisará redimensioná-los.
Plotando matrizes numpy como imagens #
Portanto, você tem seus dados em um array numpy (seja importando-o ou gerando-o). Vamos renderizar. No Matplotlib, isso é feito usando a imshow()função. Aqui vamos pegar o objeto plot. Este objeto oferece uma maneira fácil de manipular o gráfico a partir do prompt.
imgplot = plt.imshow(img)
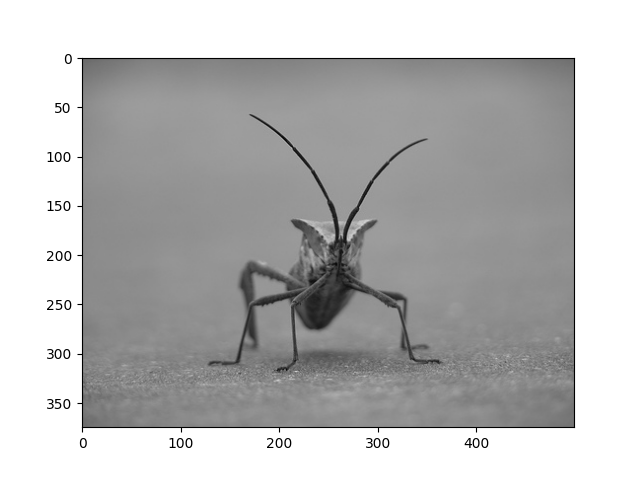
Você também pode plotar qualquer array numpy.
Aplicando esquemas de pseudocor a plotagens de imagem #
A pseudocor pode ser uma ferramenta útil para melhorar o contraste e visualizar seus dados com mais facilidade. Isso é especialmente útil ao fazer apresentações de seus dados usando projetores - seu contraste geralmente é muito ruim.
A pseudocor só é relevante para imagens de canal único, tons de cinza e luminosidade. Atualmente, temos uma imagem RGB. Como R, G e B são todos semelhantes (veja você mesmo acima ou em seus dados), podemos escolher apenas um canal de nossos dados:
lum_img = img[:, :, 0]
# This is array slicing. You can read more in the `Numpy tutorial
# <https://numpy.org/doc/stable/user/quickstart.html>`_.
plt.imshow(lum_img)
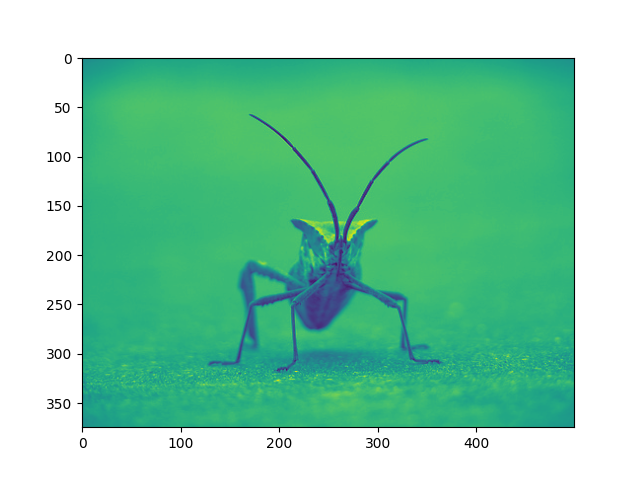
<matplotlib.image.AxesImage object at 0x7f2cdd608610>
Agora, com uma imagem de luminosidade (2D, sem cor), o mapa de cores padrão (também conhecido como tabela de pesquisa, LUT) é aplicado. O padrão é chamado viridis. Há muitos outros para escolher.
plt.imshow(lum_img, cmap="hot")
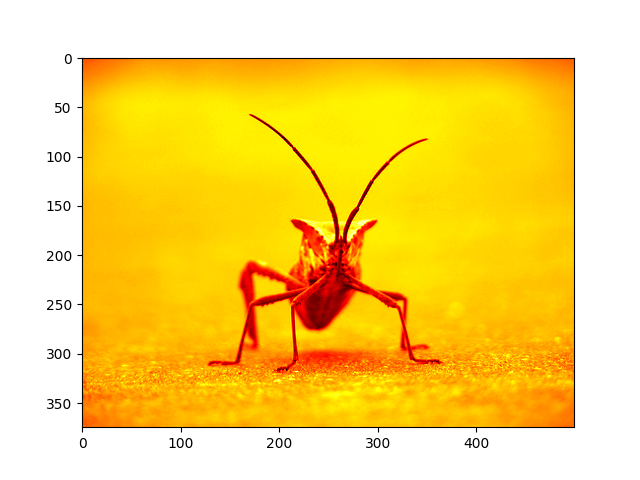
<matplotlib.image.AxesImage object at 0x7f2cddcc2aa0>
Observe que você também pode alterar mapas de cores em objetos de plotagem existentes usando o
set_cmap()método:
imgplot = plt.imshow(lum_img)
imgplot.set_cmap('nipy_spectral')
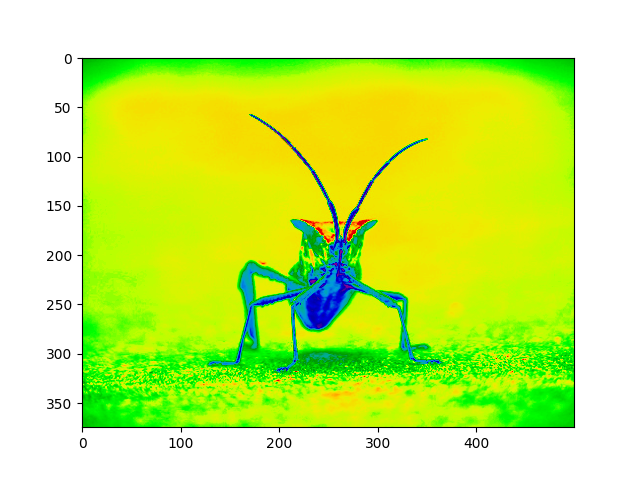
Observação
No entanto, lembre-se de que no Jupyter Notebook com back-end embutido, você não pode fazer alterações em plotagens que já foram renderizadas. Se você criar imgplot aqui em uma célula, não poderá chamar set_cmap() em uma célula posterior e esperar que o gráfico anterior seja alterado. Certifique-se de inserir esses comandos juntos em uma célula. Os comandos plt não alterarão os gráficos das células anteriores.
Existem muitos outros esquemas de mapa de cores disponíveis. Veja a lista e imagens dos mapas de cores .
Referência da escala de cores #
É útil ter uma ideia do valor que uma cor representa. Podemos fazer isso adicionando uma barra de cores à sua figura:
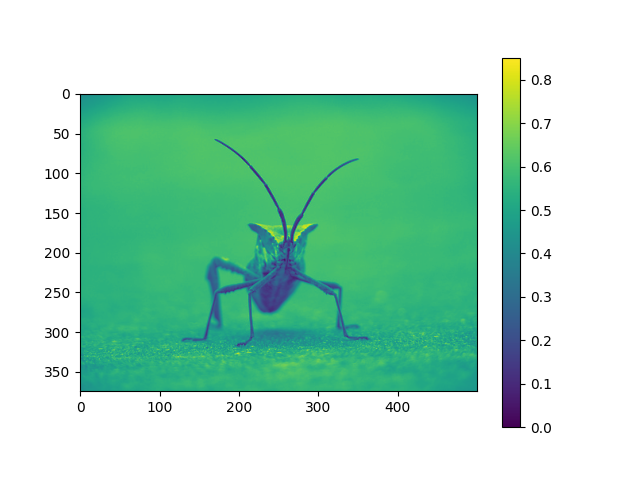
<matplotlib.colorbar.Colorbar object at 0x7f2cdf5297e0>
Examinando um intervalo de dados específico #
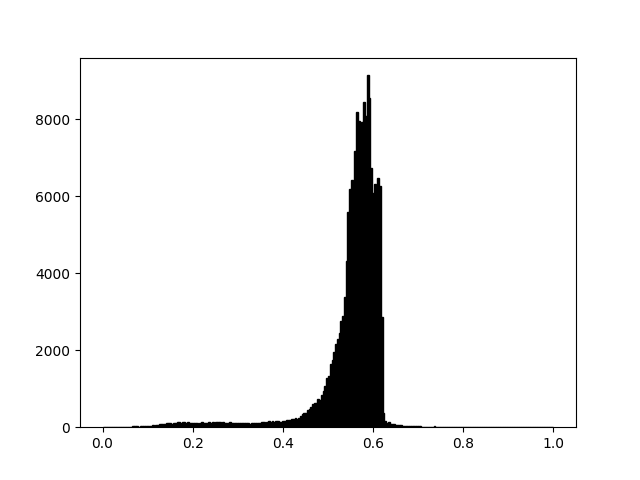
Às vezes, você deseja aumentar o contraste em sua imagem ou expandir o contraste em uma região específica, sacrificando os detalhes em cores que não variam muito ou não importam. Uma boa ferramenta para encontrar regiões interessantes é o histograma. Para criar um histograma de nossos dados de imagem, usamos a hist()função.
(array([2.000e+00, 2.000e+00, 3.000e+00, 3.000e+00, 2.000e+00, 2.000e+00,
3.000e+00, 1.000e+00, 7.000e+00, 9.000e+00, 7.000e+00, 2.000e+00,
7.000e+00, 1.000e+01, 1.100e+01, 1.500e+01, 1.400e+01, 2.700e+01,
2.100e+01, 2.400e+01, 1.400e+01, 3.100e+01, 2.900e+01, 2.800e+01,
2.400e+01, 2.400e+01, 4.000e+01, 2.600e+01, 5.200e+01, 3.900e+01,
5.700e+01, 4.600e+01, 8.400e+01, 7.600e+01, 8.900e+01, 8.000e+01,
1.060e+02, 1.130e+02, 1.120e+02, 9.000e+01, 1.160e+02, 1.090e+02,
1.270e+02, 1.350e+02, 9.800e+01, 1.310e+02, 1.230e+02, 1.110e+02,
1.230e+02, 1.160e+02, 1.010e+02, 1.170e+02, 1.000e+02, 1.010e+02,
9.000e+01, 1.060e+02, 1.260e+02, 1.040e+02, 1.070e+02, 1.110e+02,
1.380e+02, 1.000e+02, 1.340e+02, 1.210e+02, 1.400e+02, 1.320e+02,
1.390e+02, 1.160e+02, 1.330e+02, 1.180e+02, 1.080e+02, 1.170e+02,
1.280e+02, 1.200e+02, 1.210e+02, 1.100e+02, 1.160e+02, 1.180e+02,
9.700e+01, 9.700e+01, 1.140e+02, 1.070e+02, 1.170e+02, 8.700e+01,
1.070e+02, 9.800e+01, 1.040e+02, 1.120e+02, 1.110e+02, 1.180e+02,
1.240e+02, 1.340e+02, 1.200e+02, 1.410e+02, 1.520e+02, 1.360e+02,
1.610e+02, 1.380e+02, 1.620e+02, 1.570e+02, 1.350e+02, 1.470e+02,
1.690e+02, 1.710e+02, 1.820e+02, 1.980e+02, 1.970e+02, 2.060e+02,
2.160e+02, 2.460e+02, 2.210e+02, 2.520e+02, 2.890e+02, 3.450e+02,
3.620e+02, 3.760e+02, 4.480e+02, 4.630e+02, 5.170e+02, 6.000e+02,
6.200e+02, 6.410e+02, 7.440e+02, 7.120e+02, 8.330e+02, 9.290e+02,
1.061e+03, 1.280e+03, 1.340e+03, 1.638e+03, 1.740e+03, 1.953e+03,
2.151e+03, 2.290e+03, 2.440e+03, 2.758e+03, 2.896e+03, 3.384e+03,
4.332e+03, 5.584e+03, 6.197e+03, 6.422e+03, 6.404e+03, 7.181e+03,
8.196e+03, 7.968e+03, 7.474e+03, 7.926e+03, 8.460e+03, 8.091e+03,
9.148e+03, 8.563e+03, 6.747e+03, 6.074e+03, 6.328e+03, 5.291e+03,
6.472e+03, 6.268e+03, 2.864e+03, 3.760e+02, 1.620e+02, 1.180e+02,
1.270e+02, 9.500e+01, 7.600e+01, 8.200e+01, 6.200e+01, 6.700e+01,
5.600e+01, 5.900e+01, 4.000e+01, 4.200e+01, 3.000e+01, 3.400e+01,
3.200e+01, 4.300e+01, 4.200e+01, 2.300e+01, 2.800e+01, 1.900e+01,
2.200e+01, 1.600e+01, 1.200e+01, 1.800e+01, 9.000e+00, 1.000e+01,
1.700e+01, 5.000e+00, 2.100e+01, 1.300e+01, 8.000e+00, 1.200e+01,
1.000e+01, 8.000e+00, 8.000e+00, 5.000e+00, 1.300e+01, 6.000e+00,
3.000e+00, 7.000e+00, 6.000e+00, 2.000e+00, 1.000e+00, 5.000e+00,
3.000e+00, 3.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 5.000e+00,
0.000e+00, 1.000e+00, 3.000e+00, 0.000e+00, 1.000e+00, 1.000e+00,
2.000e+00, 1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00]), array([0. , 0.00390625, 0.0078125 , 0.01171875, 0.015625 ,
0.01953125, 0.0234375 , 0.02734375, 0.03125 , 0.03515625,
0.0390625 , 0.04296875, 0.046875 , 0.05078125, 0.0546875 ,
0.05859375, 0.0625 , 0.06640625, 0.0703125 , 0.07421875,
0.078125 , 0.08203125, 0.0859375 , 0.08984375, 0.09375 ,
0.09765625, 0.1015625 , 0.10546875, 0.109375 , 0.11328125,
0.1171875 , 0.12109375, 0.125 , 0.12890625, 0.1328125 ,
0.13671875, 0.140625 , 0.14453125, 0.1484375 , 0.15234375,
0.15625 , 0.16015625, 0.1640625 , 0.16796875, 0.171875 ,
0.17578125, 0.1796875 , 0.18359375, 0.1875 , 0.19140625,
0.1953125 , 0.19921875, 0.203125 , 0.20703125, 0.2109375 ,
0.21484375, 0.21875 , 0.22265625, 0.2265625 , 0.23046875,
0.234375 , 0.23828125, 0.2421875 , 0.24609375, 0.25 ,
0.25390625, 0.2578125 , 0.26171875, 0.265625 , 0.26953125,
0.2734375 , 0.27734375, 0.28125 , 0.28515625, 0.2890625 ,
0.29296875, 0.296875 , 0.30078125, 0.3046875 , 0.30859375,
0.3125 , 0.31640625, 0.3203125 , 0.32421875, 0.328125 ,
0.33203125, 0.3359375 , 0.33984375, 0.34375 , 0.34765625,
0.3515625 , 0.35546875, 0.359375 , 0.36328125, 0.3671875 ,
0.37109375, 0.375 , 0.37890625, 0.3828125 , 0.38671875,
0.390625 , 0.39453125, 0.3984375 , 0.40234375, 0.40625 ,
0.41015625, 0.4140625 , 0.41796875, 0.421875 , 0.42578125,
0.4296875 , 0.43359375, 0.4375 , 0.44140625, 0.4453125 ,
0.44921875, 0.453125 , 0.45703125, 0.4609375 , 0.46484375,
0.46875 , 0.47265625, 0.4765625 , 0.48046875, 0.484375 ,
0.48828125, 0.4921875 , 0.49609375, 0.5 , 0.50390625,
0.5078125 , 0.51171875, 0.515625 , 0.51953125, 0.5234375 ,
0.52734375, 0.53125 , 0.53515625, 0.5390625 , 0.54296875,
0.546875 , 0.55078125, 0.5546875 , 0.55859375, 0.5625 ,
0.56640625, 0.5703125 , 0.57421875, 0.578125 , 0.58203125,
0.5859375 , 0.58984375, 0.59375 , 0.59765625, 0.6015625 ,
0.60546875, 0.609375 , 0.61328125, 0.6171875 , 0.62109375,
0.625 , 0.62890625, 0.6328125 , 0.63671875, 0.640625 ,
0.64453125, 0.6484375 , 0.65234375, 0.65625 , 0.66015625,
0.6640625 , 0.66796875, 0.671875 , 0.67578125, 0.6796875 ,
0.68359375, 0.6875 , 0.69140625, 0.6953125 , 0.69921875,
0.703125 , 0.70703125, 0.7109375 , 0.71484375, 0.71875 ,
0.72265625, 0.7265625 , 0.73046875, 0.734375 , 0.73828125,
0.7421875 , 0.74609375, 0.75 , 0.75390625, 0.7578125 ,
0.76171875, 0.765625 , 0.76953125, 0.7734375 , 0.77734375,
0.78125 , 0.78515625, 0.7890625 , 0.79296875, 0.796875 ,
0.80078125, 0.8046875 , 0.80859375, 0.8125 , 0.81640625,
0.8203125 , 0.82421875, 0.828125 , 0.83203125, 0.8359375 ,
0.83984375, 0.84375 , 0.84765625, 0.8515625 , 0.85546875,
0.859375 , 0.86328125, 0.8671875 , 0.87109375, 0.875 ,
0.87890625, 0.8828125 , 0.88671875, 0.890625 , 0.89453125,
0.8984375 , 0.90234375, 0.90625 , 0.91015625, 0.9140625 ,
0.91796875, 0.921875 , 0.92578125, 0.9296875 , 0.93359375,
0.9375 , 0.94140625, 0.9453125 , 0.94921875, 0.953125 ,
0.95703125, 0.9609375 , 0.96484375, 0.96875 , 0.97265625,
0.9765625 , 0.98046875, 0.984375 , 0.98828125, 0.9921875 ,
0.99609375, 1. ]), <BarContainer object of 256 artists>)
Na maioria das vezes, a parte "interessante" da imagem está em torno do pico e você pode obter um contraste extra recortando as regiões acima e/ou abaixo do pico. Em nosso histograma, parece que não há muita informação útil no high-end (não há muitas coisas brancas na imagem). Vamos ajustar o limite superior, para que efetivamente "ampliemos" parte do histograma. Fazemos isso passando o argumento clim para imshow. Você também pode fazer isso chamando o
set_clim()método do objeto de plotagem de imagem, mas certifique-se de fazê-lo na mesma célula que seu comando de plotagem ao trabalhar com o Jupyter Notebook - ele não alterará as plotagens das células anteriores.
Você pode especificar o clim na chamada para plot.
imgplot = plt.imshow(lum_img, clim=(0.0, 0.7))
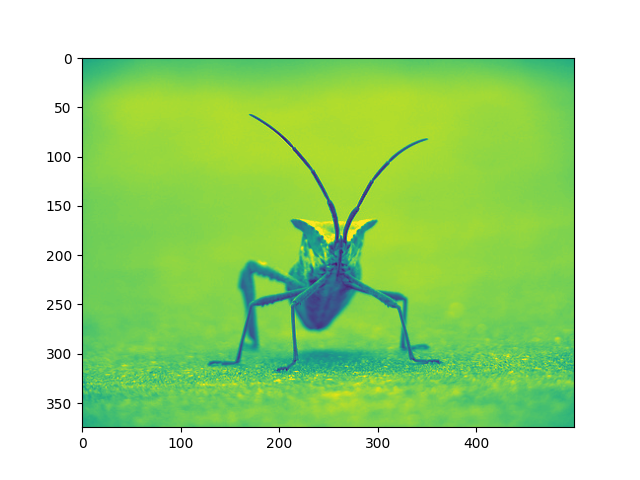
Você também pode especificar o clim usando o objeto retornado
fig = plt.figure()
ax = fig.add_subplot(1, 2, 1)
imgplot = plt.imshow(lum_img)
ax.set_title('Before')
plt.colorbar(ticks=[0.1, 0.3, 0.5, 0.7], orientation='horizontal')
ax = fig.add_subplot(1, 2, 2)
imgplot = plt.imshow(lum_img)
imgplot.set_clim(0.0, 0.7)
ax.set_title('After')
plt.colorbar(ticks=[0.1, 0.3, 0.5, 0.7], orientation='horizontal')
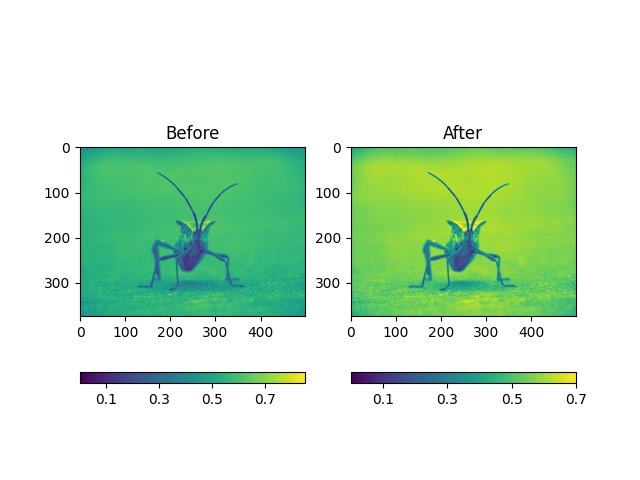
<matplotlib.colorbar.Colorbar object at 0x7f2cdf75fa30>
Esquemas de interpolação de matriz #
A interpolação calcula qual a cor ou valor de um pixel "deveria" ser, de acordo com diferentes esquemas matemáticos. Um lugar comum em que isso acontece é quando você redimensiona uma imagem. O número de pixels muda, mas você deseja as mesmas informações. Como os pixels são discretos, falta espaço. A interpolação é como você preenche esse espaço. É por isso que suas imagens às vezes parecem pixelizadas quando você as amplia. O efeito é mais pronunciado quando a diferença entre a imagem original e a imagem expandida é maior. Vamos pegar nossa imagem e reduzi-la. Estamos efetivamente descartando pixels, mantendo apenas alguns selecionados. Agora, quando plotamos, esses dados são ampliados para o tamanho da tela. Os pixels antigos não estão mais lá e o computador precisa desenhar pixels para preencher esse espaço.
Usaremos a biblioteca Pillow que usamos para carregar a imagem também para redimensionar a imagem.
from PIL import Image
img = Image.open('../../doc/_static/stinkbug.png')
img.thumbnail((64, 64)) # resizes image in-place
imgplot = plt.imshow(img)
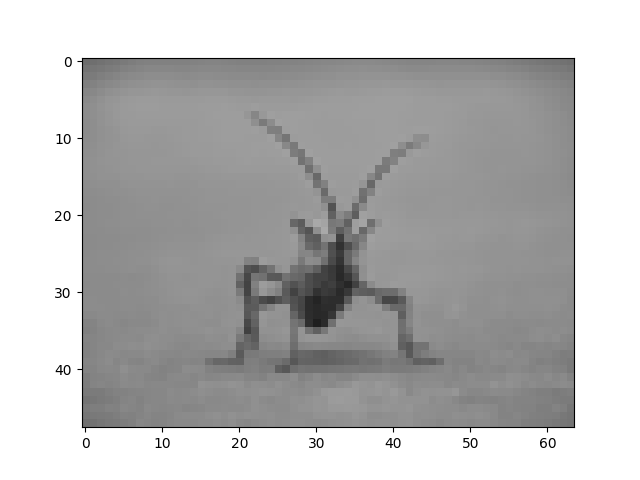
Aqui temos a interpolação padrão, bilinear, pois não fornecemos imshow()nenhum argumento de interpolação.
Vamos tentar alguns outros. Aqui está "mais próximo", que não faz interpolação.
imgplot = plt.imshow(img, interpolation="nearest")
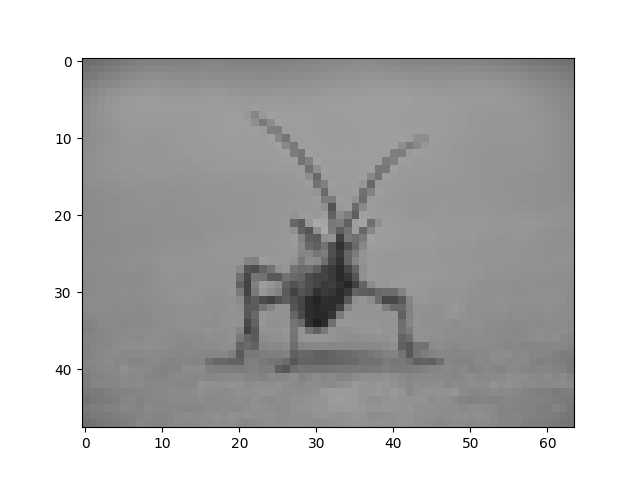
e bicúbico:
imgplot = plt.imshow(img, interpolation="bicubic")
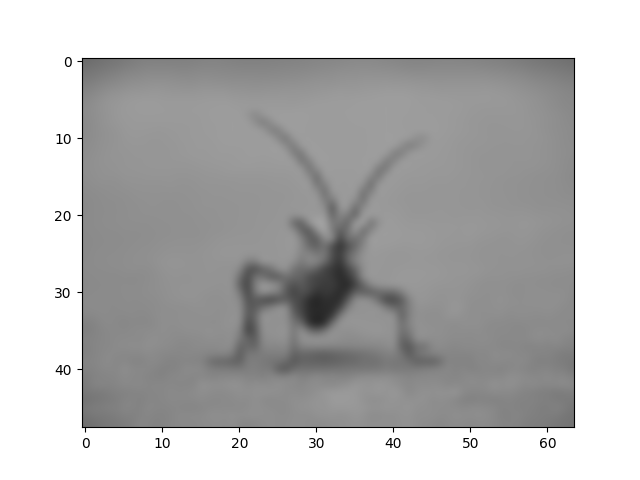
A interpolação bicúbica é frequentemente usada ao ampliar fotos - as pessoas tendem a preferir borradas a pixeladas.
Tempo total de execução do script: ( 0 minutos 8,344 segundos)