Tipos de projeção de plotagem 3D

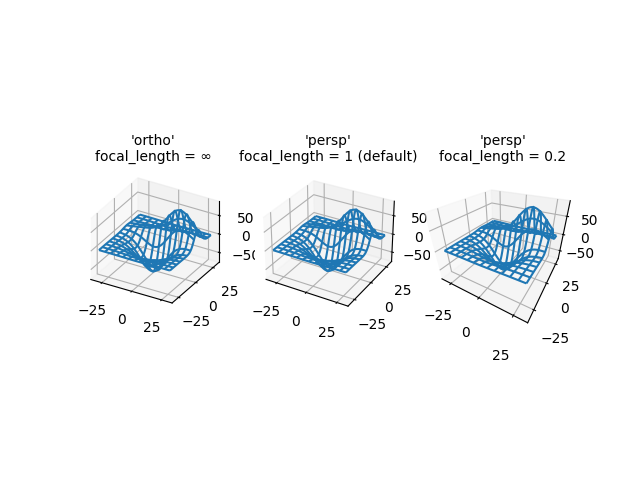
Demonstra as diferentes projeções de câmera para plotagens 3D e os efeitos da alteração da distância focal para uma projeção em perspectiva. Observe que o Matplotlib corrige o efeito 'zoom' da alteração da distância focal.

A distância focal padrão de 1 corresponde a um campo de visão (FOV) de 90 graus. Uma distância focal aumentada entre 1 e infinito "achata" a imagem, enquanto uma distância focal diminuída entre 1 e 0 exagera a perspectiva e dá à imagem uma profundidade mais aparente. No caso limite, uma distância focal de infinito corresponde a uma projeção ortográfica após a correção do efeito de zoom.

Você pode calcular a distância focal de um FOV através da equação:

\[1 / \tan (\mathrm{FOV} / 2)\]

Ou vice-versa:

\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{focal length})\]

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt


fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})

# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot the data
for ax in axs:
    ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

# Set the orthographic projection.
axs[0].set_proj_type('ortho')  # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)

# Set the perspective projections
axs[1].set_proj_type('persp')  # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)

axs[2].set_proj_type('persp', focal_length=0.2)  # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)

plt.show()