Asinh Demo #

Ilustração da asinhescala do eixo, que usa a transformação

\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]

Para valores de coordenadas próximos de zero (ou seja, muito menores que a "largura linear"\(a_0\)), isso deixa os valores essencialmente inalterados:

\[a \rightarrow a + \mathcal{O}(a^3)\]

mas para valores maiores (isto é\(|a| \gg a_0\), isso é assintoticamente

\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]

Tal como acontece com o symlogdimensionamento, isso permite plotar quantidades que cobrem uma faixa dinâmica muito ampla que inclui valores positivos e negativos. No entanto, symlogenvolve uma transformação que possui descontinuidades em seu gradiente porque é construída a partir de transformações lineares e logarítmicas separadas . O asinhdimensionamento usa uma transformação suave para todos os valores (finitos), que é matematicamente mais limpo e reduz os artefatos visuais associados a uma transição abrupta entre regiões lineares e logarítmicas do gráfico.

Observação

scale.AsinhScaleé experimental e a API pode mudar.

Veja AsinhScale, SymmetricalLogScale.

import numpy as np
import matplotlib.pyplot as plt

# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)

Compare o comportamento "symlog" e "asinh" no gráfico de amostra y=x, onde há um gradiente descontínuo em "symlog" perto de y=2:

fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)

ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')

ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')

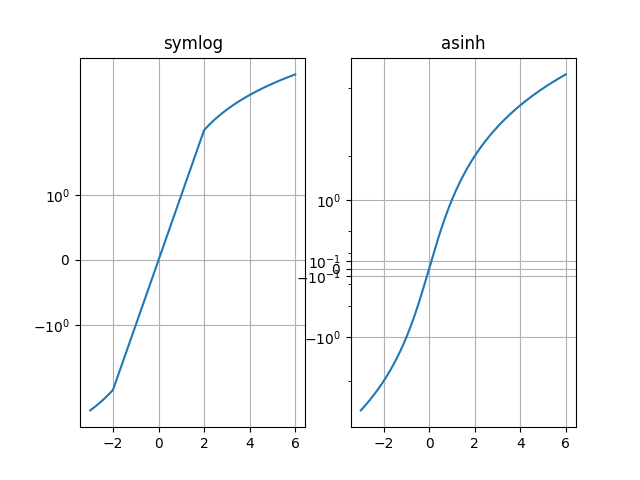
Text(0.5, 1.0, 'asinh')

Compare gráficos "asinh" com diferentes parâmetros de escala "linear_width":

fig2 = plt.figure(constrained_layout=True)
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
    ax.set_title('linear_width={:.3g}'.format(a0))
    ax.plot(x, x, label='y=x')
    ax.plot(x, 10*x, label='y=10x')
    ax.plot(x, 100*x, label='y=100x')
    ax.set_yscale('asinh', linear_width=a0, base=base)
    ax.grid()
    ax.legend(loc='best', fontsize='small')

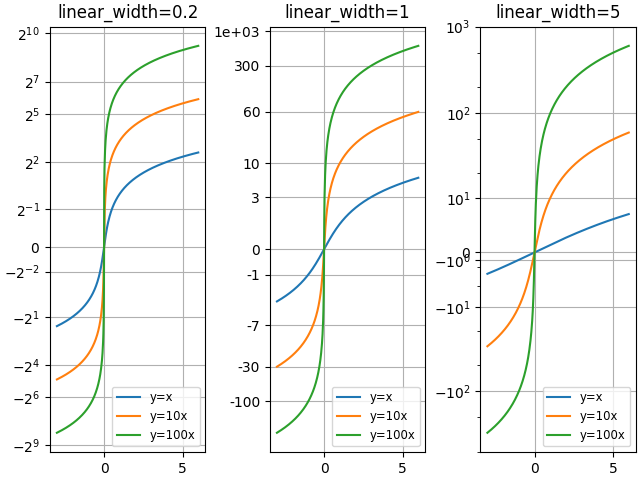
linear_width=0,2, linear_width=1, linear_width=5

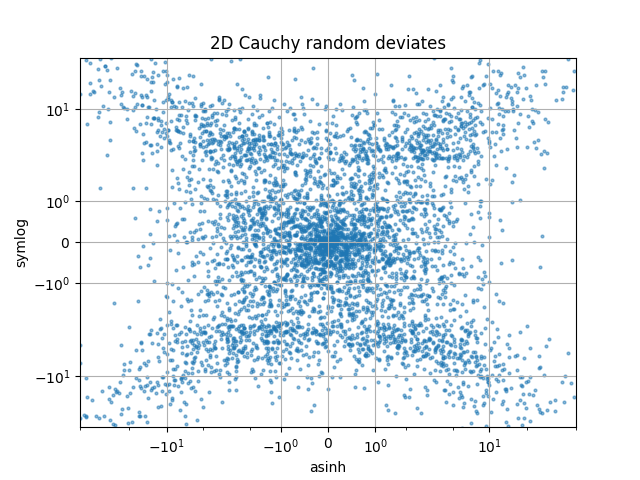
Compare as escalas "symlog" e "asinh" em números aleatórios 2D distribuídos por Cauchy, onde é possível ver artefatos mais sutis perto de y=2 devido à descontinuidade de gradiente em "symlog":

fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
                                 size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)

ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()

plt.show()

Referências

Tempo total de execução do script: ( 0 minutos 2,229 segundos)

Galeria gerada por Sphinx-Gallery