Observação
Clique aqui para baixar o código de exemplo completo
Normalizações do mapa de cores #
Demonstração do uso de norma para mapear mapas de cores em dados de maneiras não lineares.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
Lognorm: Em vez de pcolor log10(Z1), você pode ter barras de cores com rótulos exponenciais usando uma norma.
N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
# A low hump with a spike coming out of the top. Needs to have
# z/colour axis on a log scale so we see both hump and spike. linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolor(X, Y, Z,
norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='max')
pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='max')
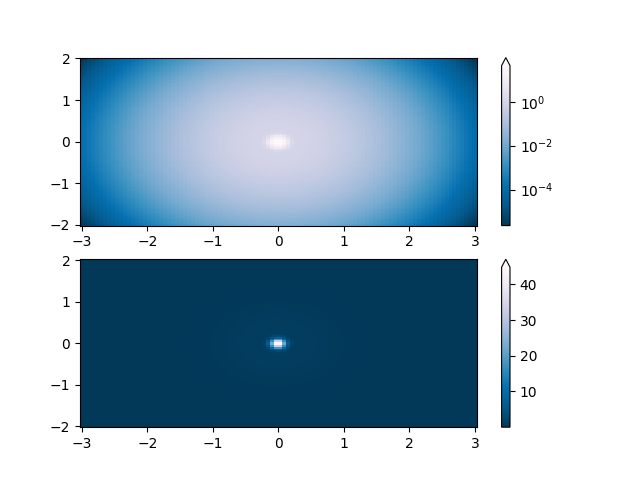
<matplotlib.colorbar.Colorbar object at 0x7f2cfb030d90>
PowerNorm: Aqui, uma tendência de lei de potência em X obscurece parcialmente uma onda senoidal retificada em Y. Podemos remover a lei de potência usando uma PowerNorm.
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=1. / 2.),
cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='max')
pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='max')
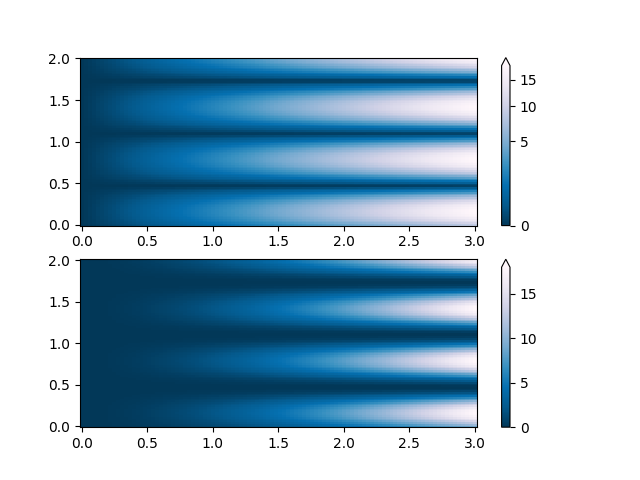
<matplotlib.colorbar.Colorbar object at 0x7f2cfb4f44c0>
SymLogNorm: dois picos, um negativo e um positivo, o positivo com 5 vezes a amplitude. Linearmente, você não pode ver detalhes na protuberância negativa. Aqui escalamos logaritmicamente os dados positivos e negativos separadamente.
Observe que os rótulos da barra de cores não parecem muito bons.
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = 5 * np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z1,
norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
vmin=-1.0, vmax=1.0, base=10),
cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='both')
pcm = ax[1].pcolormesh(X, Y, Z1, cmap='RdBu_r', vmin=-np.max(Z1),
shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='both')
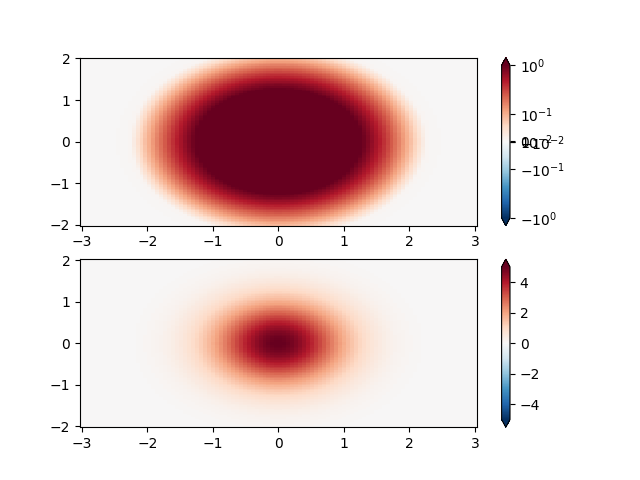
<matplotlib.colorbar.Colorbar object at 0x7f2cfb59c9a0>
Norma personalizada: um exemplo com uma normalização personalizada. Este usa o exemplo acima e normaliza os dados negativos de maneira diferente dos positivos.
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2
# Example of making your own norm. Also see matplotlib.colors.
# From Joe Kington: This one gives two different linear ramps:
class MidpointNormalize(colors.Normalize):
def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
self.midpoint = midpoint
super().__init__(vmin, vmax, clip)
def __call__(self, value, clip=None):
# I'm ignoring masked values and all kinds of edge cases to make a
# simple example...
x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
return np.ma.masked_array(np.interp(value, x, y))
#####
fig, ax = plt.subplots(2, 1)
pcm = ax[0].pcolormesh(X, Y, Z,
norm=MidpointNormalize(midpoint=0.),
cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='both')
pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z),
shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='both')
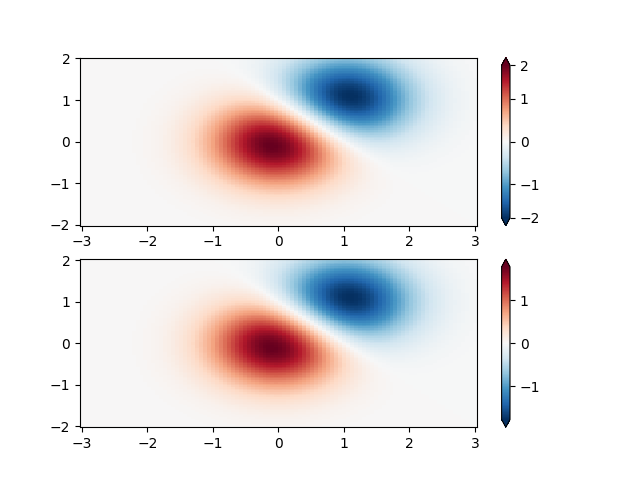
<matplotlib.colorbar.Colorbar object at 0x7f2cfb533910>
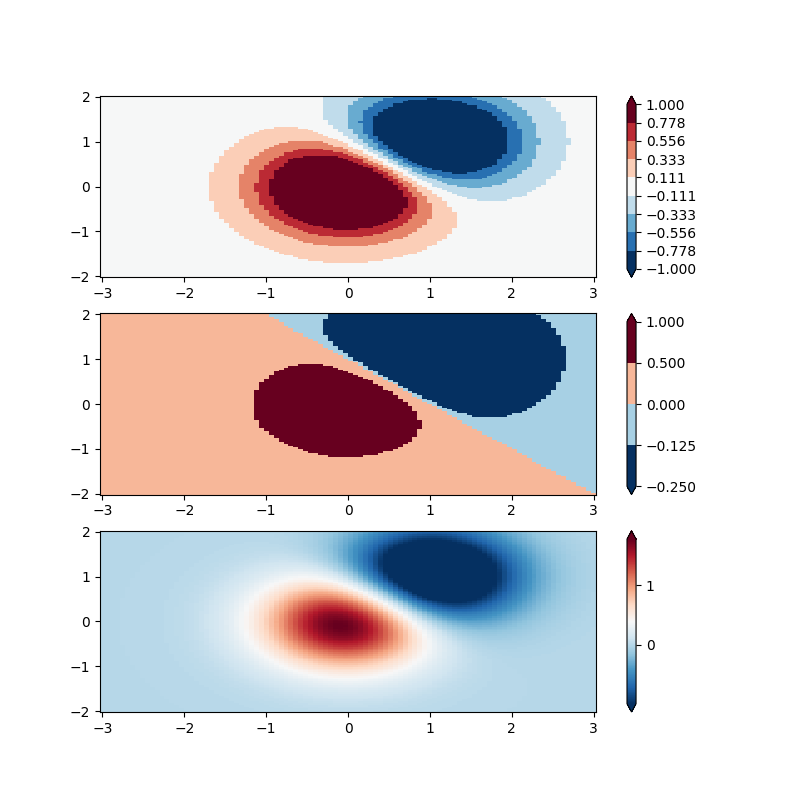
BoundaryNorm: Para este você fornece os limites para suas cores, e o Norm coloca a primeira cor entre o primeiro par, a segunda cor entre o segundo par, etc.
fig, ax = plt.subplots(3, 1, figsize=(8, 8))
ax = ax.flatten()
# even bounds gives a contour-like effect
bounds = np.linspace(-1, 1, 10)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[0].pcolormesh(X, Y, Z,
norm=norm,
cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[0], extend='both', orientation='vertical')
# uneven bounds changes the colormapping:
bounds = np.array([-0.25, -0.125, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r', shading='nearest')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
pcm = ax[2].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z1),
shading='nearest')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
plt.show()
Tempo total de execução do script: (0 minutos 3,715 segundos)