Observação
Clique aqui para baixar o código de exemplo completo
Renderizando equações matemáticas usando o TeX #
Você pode usar o TeX para renderizar todo o texto do Matplotlib definindo
rcParams["text.usetex"](padrão: False) como True. Isso requer que você tenha o TeX e as outras dependências descritas no tutorial Renderização de texto com LaTeX instalado corretamente em seu sistema. O Matplotlib armazena em cache as expressões TeX processadas, de modo que apenas a primeira ocorrência de uma expressão acione uma compilação TeX. As ocorrências posteriores reutilizam a imagem renderizada do cache e, portanto, são mais rápidas.
A entrada Unicode é suportada, por exemplo, para o rótulo do eixo y neste exemplo.
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['text.usetex'] = True
t = np.linspace(0.0, 1.0, 100)
s = np.cos(4 * np.pi * t) + 2
fig, ax = plt.subplots(figsize=(6, 4), tight_layout=True)
ax.plot(t, s)
ax.set_xlabel(r'\textbf{time (s)}')
ax.set_ylabel('\\textit{Velocity (\N{DEGREE SIGN}/sec)}', fontsize=16)
ax.set_title(r'\TeX\ is Number $\displaystyle\sum_{n=1}^\infty'
r'\frac{-e^{i\pi}}{2^n}$!', fontsize=16, color='r')
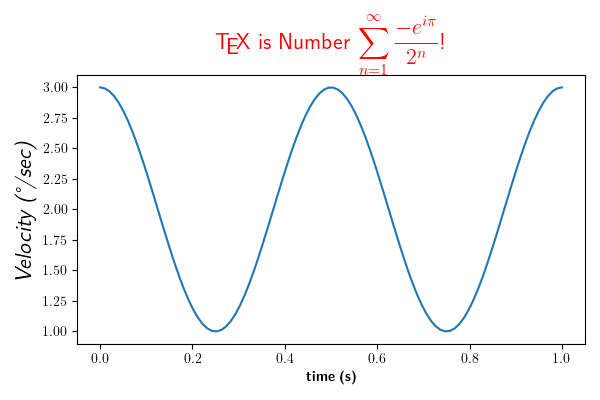
Text(0.5, 1.0652809399537557, '\\TeX\\ is Number $\\displaystyle\\sum_{n=1}^\\infty\\frac{-e^{i\\pi}}{2^n}$!')
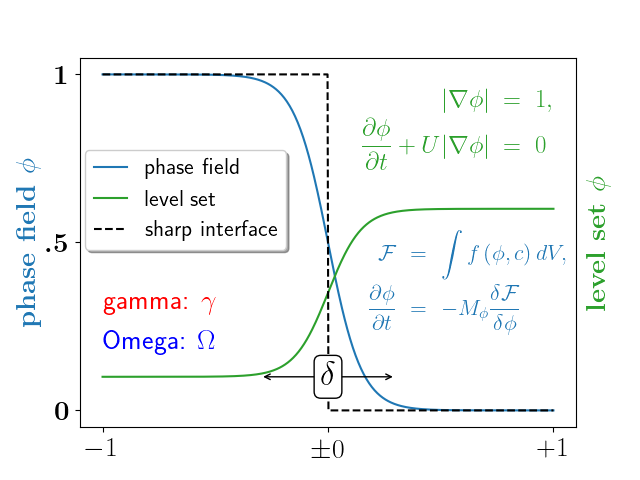
Um exemplo mais complexo.
fig, ax = plt.subplots()
# interface tracking profiles
N = 500
delta = 0.6
X = np.linspace(-1, 1, N)
ax.plot(X, (1 - np.tanh(4 * X / delta)) / 2, # phase field tanh profiles
X, (1.4 + np.tanh(4 * X / delta)) / 4, "C2", # composition profile
X, X < 0, "k--") # sharp interface
# legend
ax.legend(("phase field", "level set", "sharp interface"),
shadow=True, loc=(0.01, 0.48), handlelength=1.5, fontsize=16)
# the arrow
ax.annotate("", xy=(-delta / 2., 0.1), xytext=(delta / 2., 0.1),
arrowprops=dict(arrowstyle="<->", connectionstyle="arc3"))
ax.text(0, 0.1, r"$\delta$",
color="black", fontsize=24,
horizontalalignment="center", verticalalignment="center",
bbox=dict(boxstyle="round", fc="white", ec="black", pad=0.2))
# Use tex in labels
ax.set_xticks([-1, 0, 1])
ax.set_xticklabels(["$-1$", r"$\pm 0$", "$+1$"], color="k", size=20)
# Left Y-axis labels, combine math mode and text mode
ax.set_ylabel(r"\bf{phase field} $\phi$", color="C0", fontsize=20)
ax.set_yticks([0, 0.5, 1])
ax.set_yticklabels([r"\bf{0}", r"\bf{.5}", r"\bf{1}"], color="k", size=20)
# Right Y-axis labels
ax.text(1.02, 0.5, r"\bf{level set} $\phi$",
color="C2", fontsize=20, rotation=90,
horizontalalignment="left", verticalalignment="center",
clip_on=False, transform=ax.transAxes)
# Use multiline environment inside a `text`.
# level set equations
eq1 = (r"\begin{eqnarray*}"
r"|\nabla\phi| &=& 1,\\"
r"\frac{\partial \phi}{\partial t} + U|\nabla \phi| &=& 0 "
r"\end{eqnarray*}")
ax.text(1, 0.9, eq1, color="C2", fontsize=18,
horizontalalignment="right", verticalalignment="top")
# phase field equations
eq2 = (r"\begin{eqnarray*}"
r"\mathcal{F} &=& \int f\left( \phi, c \right) dV, \\ "
r"\frac{ \partial \phi } { \partial t } &=& -M_{ \phi } "
r"\frac{ \delta \mathcal{F} } { \delta \phi }"
r"\end{eqnarray*}")
ax.text(0.18, 0.18, eq2, color="C0", fontsize=16)
ax.text(-1, .30, r"gamma: $\gamma$", color="r", fontsize=20)
ax.text(-1, .18, r"Omega: $\Omega$", color="b", fontsize=20)
plt.show()
Tempo total de execução do script: ( 0 minutos 1,076 segundos)