Preencher entre e alfa

A fill_betweenfunção gera uma região sombreada entre um limite mínimo e máximo que é útil para ilustrar intervalos. Ele tem um argumento muito útil wherepara combinar o preenchimento com intervalos lógicos, por exemplo, apenas para preencher uma curva acima de algum valor limite.

Em seu nível mais básico, fill_betweenpode ser usado para aprimorar a aparência visual de um gráfico. Vamos comparar dois gráficos de dados financeiros com um gráfico de linha simples à esquerda e uma linha preenchida à direita.

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.cbook as cbook


# load up some sample financial data
r = (cbook.get_sample_data('goog.npz', np_load=True)['price_data']
     .view(np.recarray))
# create two subplots with the shared x and y axes
fig, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True)

pricemin = r.close.min()

ax1.plot(r.date, r.close, lw=2)
ax2.fill_between(r.date, pricemin, r.close, alpha=0.7)

for ax in ax1, ax2:
    ax.grid(True)
    ax.label_outer()

ax1.set_ylabel('price')

fig.suptitle('Google (GOOG) daily closing price')
fig.autofmt_xdate()

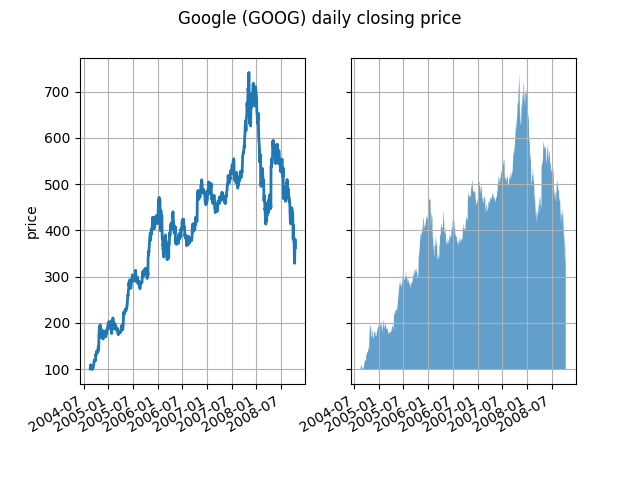
O canal alfa não é necessário aqui, mas pode ser usado para suavizar cores para gráficos mais atraentes visualmente. Em outros exemplos, como veremos a seguir, o canal alfa é funcionalmente útil, pois as regiões sombreadas podem se sobrepor e o alfa permite que você veja ambas. Observe que o formato postscript não suporta alfa (esta é uma limitação do postscript, não uma limitação do matplotlib), portanto, ao usar o alfa, salve suas figuras em PNG, PDF ou SVG.

Nosso próximo exemplo calcula duas populações de caminhantes aleatórios com média e desvio padrão diferentes das distribuições normais das quais os passos são extraídos. Usamos regiões preenchidas para plotar +/- um desvio padrão da posição média da população. Aqui o canal alfa é útil, não apenas estético.

# Fixing random state for reproducibility
np.random.seed(19680801)

Nsteps, Nwalkers = 100, 250
t = np.arange(Nsteps)

# an (Nsteps x Nwalkers) array of random walk steps
S1 = 0.004 + 0.02*np.random.randn(Nsteps, Nwalkers)
S2 = 0.002 + 0.01*np.random.randn(Nsteps, Nwalkers)

# an (Nsteps x Nwalkers) array of random walker positions
X1 = S1.cumsum(axis=0)
X2 = S2.cumsum(axis=0)


# Nsteps length arrays empirical means and standard deviations of both
# populations over time
mu1 = X1.mean(axis=1)
sigma1 = X1.std(axis=1)
mu2 = X2.mean(axis=1)
sigma2 = X2.std(axis=1)

# plot it!
fig, ax = plt.subplots(1)
ax.plot(t, mu1, lw=2, label='mean population 1')
ax.plot(t, mu2, lw=2, label='mean population 2')
ax.fill_between(t, mu1+sigma1, mu1-sigma1, facecolor='C0', alpha=0.4)
ax.fill_between(t, mu2+sigma2, mu2-sigma2, facecolor='C1', alpha=0.4)
ax.set_title(r'random walkers empirical $\mu$ and $\pm \sigma$ interval')
ax.legend(loc='upper left')
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

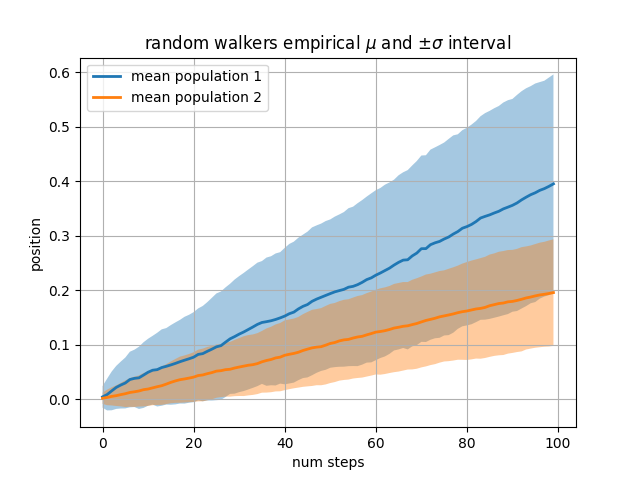
O whereargumento de palavra-chave é muito útil para destacar certas regiões do gráfico. wheretoma uma máscara booleana do mesmo comprimento que os argumentos x, ymin e ymax, e só preenche a região onde a máscara booleana é True. No exemplo abaixo, simulamos um único caminhante aleatório e calculamos a média analítica e o desvio padrão das posições da população. A média da população é mostrada como a linha tracejada, e o desvio mais/menos um sigma da média é mostrado como a região preenchida. Usamos a máscara where para encontrar a região onde o caminhante está fora do limite de um sigma e sombreamos essa região de vermelho.X > upper_bound

# Fixing random state for reproducibility
np.random.seed(1)

Nsteps = 500
t = np.arange(Nsteps)

mu = 0.002
sigma = 0.01

# the steps and position
S = mu + sigma*np.random.randn(Nsteps)
X = S.cumsum()

# the 1 sigma upper and lower analytic population bounds
lower_bound = mu*t - sigma*np.sqrt(t)
upper_bound = mu*t + sigma*np.sqrt(t)

fig, ax = plt.subplots(1)
ax.plot(t, X, lw=2, label='walker position')
ax.plot(t, mu*t, lw=1, label='population mean', color='C0', ls='--')
ax.fill_between(t, lower_bound, upper_bound, facecolor='C0', alpha=0.4,
                label='1 sigma range')
ax.legend(loc='upper left')

# here we use the where argument to only fill the region where the
# walker is above the population 1 sigma boundary
ax.fill_between(t, upper_bound, X, where=X > upper_bound, fc='red', alpha=0.4)
ax.fill_between(t, lower_bound, X, where=X < lower_bound, fc='red', alpha=0.4)
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

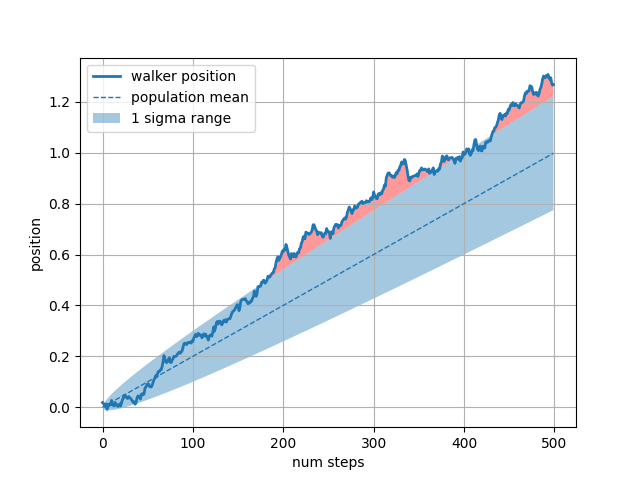
Outro uso útil de regiões preenchidas é destacar extensões horizontais ou verticais de um eixo - para isso, o Matplotlib tem as funções auxiliares axhspane axvspan. Veja a demonstração do axhspan .

plt.show()