Histograma de Série Temporal #

Este exemplo demonstra como visualizar com eficiência um grande número de séries temporais de uma forma que pode potencialmente revelar subestruturas e padrões ocultos que não são imediatamente óbvios e exibi-los de maneira visualmente atraente.

Neste exemplo, geramos múltiplas séries de "sinal" senoidais que são enterradas sob um número maior de séries de "ruído/fundo" de passeio aleatório. Para um passeio aleatório Gaussiano imparcial com desvio padrão de σ, o desvio RMS da origem após n passos é σ*sqrt(n). Portanto, para manter as senoides visíveis na mesma escala dos passeios aleatórios, dimensionamos a amplitude pelo RMS do passeio aleatório. Além disso, também introduzimos um pequeno deslocamento aleatório phi para deslocar os senos para a esquerda/direita e algum ruído aleatório aditivo para deslocar pontos de dados individuais para cima/para baixo para tornar o sinal um pouco mais "realista" (você não esperaria um seno perfeito onda apareça em seus dados).

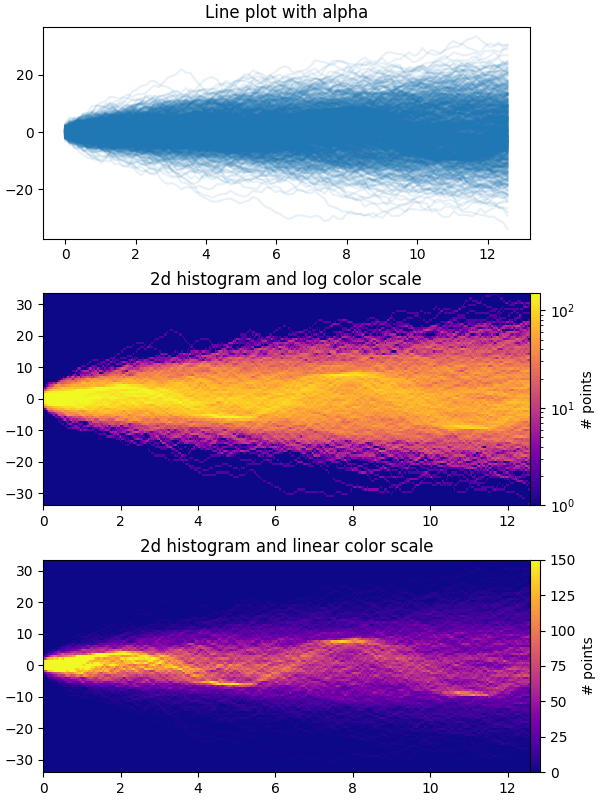
O primeiro gráfico mostra a maneira típica de visualizar várias séries temporais sobrepondo-as umas sobre as outras com plt.plote um pequeno valor de alpha. O segundo e terceiro gráficos mostram como reinterpretar os dados como um histograma 2D, com interpolação opcional entre os pontos de dados, usando np.histogram2de plt.pcolormesh.

from copy import copy
import time

import numpy as np
import numpy.matlib
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm

fig, axes = plt.subplots(nrows=3, figsize=(6, 8), constrained_layout=True)

# Make some data; a 1D random walk + small fraction of sine waves
num_series = 1000
num_points = 100
SNR = 0.10  # Signal to Noise Ratio
x = np.linspace(0, 4 * np.pi, num_points)
# Generate unbiased Gaussian random walks
Y = np.cumsum(np.random.randn(num_series, num_points), axis=-1)
# Generate sinusoidal signals
num_signal = int(round(SNR * num_series))
phi = (np.pi / 8) * np.random.randn(num_signal, 1)  # small random offset
Y[-num_signal:] = (
    np.sqrt(np.arange(num_points))[None, :]  # random walk RMS scaling factor
    * (np.sin(x[None, :] - phi)
       + 0.05 * np.random.randn(num_signal, num_points))  # small random noise
)


# Plot series using `plot` and a small value of `alpha`. With this view it is
# very difficult to observe the sinusoidal behavior because of how many
# overlapping series there are. It also takes a bit of time to run because so
# many individual artists need to be generated.
tic = time.time()
axes[0].plot(x, Y.T, color="C0", alpha=0.1)
toc = time.time()
axes[0].set_title("Line plot with alpha")
print(f"{toc-tic:.3f} sec. elapsed")


# Now we will convert the multiple time series into a histogram. Not only will
# the hidden signal be more visible, but it is also a much quicker procedure.
tic = time.time()
# Linearly interpolate between the points in each time series
num_fine = 800
x_fine = np.linspace(x.min(), x.max(), num_fine)
y_fine = np.empty((num_series, num_fine), dtype=float)
for i in range(num_series):
    y_fine[i, :] = np.interp(x_fine, x, Y[i, :])
y_fine = y_fine.flatten()
x_fine = np.matlib.repmat(x_fine, num_series, 1).flatten()


# Plot (x, y) points in 2d histogram with log colorscale
# It is pretty evident that there is some kind of structure under the noise
# You can tune vmax to make signal more visible
cmap = copy(plt.cm.plasma)
cmap.set_bad(cmap(0))
h, xedges, yedges = np.histogram2d(x_fine, y_fine, bins=[400, 100])
pcm = axes[1].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         norm=LogNorm(vmax=1.5e2), rasterized=True)
fig.colorbar(pcm, ax=axes[1], label="# points", pad=0)
axes[1].set_title("2d histogram and log color scale")

# Same data but on linear color scale
pcm = axes[2].pcolormesh(xedges, yedges, h.T, cmap=cmap,
                         vmax=1.5e2, rasterized=True)
fig.colorbar(pcm, ax=axes[2], label="# points", pad=0)
axes[2].set_title("2d histogram and linear color scale")

toc = time.time()
print(f"{toc-tic:.3f} sec. elapsed")
plt.show()

Gráfico de linhas com alfa, histograma 2d e escala de cores logarítmicas, histograma 2d e escala de cores linear

0.219 sec. elapsed
0.071 sec. elapsed

Referências

O uso das seguintes funções, métodos, classes e módulos é mostrado neste exemplo:

Tempo total de execução do script: ( 0 minutos 2,659 segundos)

Galeria gerada por Sphinx-Gallery