Criando um mapa de cores a partir de uma lista de cores #

Para obter mais detalhes sobre como criar e manipular mapas de cores, consulte Criando mapas de cores no Matplotlib .

A criação de um mapa de cores a partir de uma lista de cores pode ser feita com o LinearSegmentedColormap.from_listmétodo. Você deve passar uma lista de tuplas RGB que definem a mistura de cores de 0 a 1.

Criando mapas de cores personalizados #

Também é possível criar um mapeamento personalizado para um mapa de cores. Isso é feito criando um dicionário que especifica como os canais RGB mudam de uma extremidade do cmap para a outra.

Exemplo: suponha que você queira que o vermelho aumente de 0 para 1 na metade inferior, o verde faça o mesmo na metade intermediária e o azul na metade superior. Então você usaria:

cdict = {
    'red': (
        (0.0,  0.0, 0.0),
        (0.5,  1.0, 1.0),
        (1.0,  1.0, 1.0),
    ),
    'green': (
        (0.0,  0.0, 0.0),
        (0.25, 0.0, 0.0),
        (0.75, 1.0, 1.0),
        (1.0,  1.0, 1.0),
    ),
    'blue': (
        (0.0,  0.0, 0.0),
        (0.5,  0.0, 0.0),
        (1.0,  1.0, 1.0),
    )
}

Se, como neste exemplo, não houver descontinuidades nos componentes r, g e b, então é bem simples: o segundo e o terceiro elemento de cada tupla, acima, são os mesmos - chame-os de " y". O primeiro elemento (" x") define os intervalos de interpolação em todo o intervalo de 0 a 1 e deve abranger todo esse intervalo. Em outras palavras, os valores de xdividem o intervalo de 0 para 1 em um conjunto de segmentos e yfornecem os valores de cor do ponto final para cada segmento.

Agora considere o verde, cdict['green']está dizendo isso para:

0 <= x<= 0,25, yé zero; sem verde.
0,25 < x<= 0,75, yvaria linearmente de 0 a 1.
0,75 < x<= 1, ypermanece em 1, totalmente verde.

Se houver descontinuidades, então é um pouco mais complicado. Rotule os 3 elementos em cada linha na cdictentrada para uma determinada cor como . Então, para valores entre e o valor da cor é interpolado entre e .(x, y0, y1)xx[i]x[i+1]y1[i]y0[i+1]

Voltando ao exemplo de um livro de receitas:

cdict = {
    'red': (
        (0.0,  0.0, 0.0),
        (0.5,  1.0, 0.7),
        (1.0,  1.0, 1.0),
    ),
    'green': (
        (0.0,  0.0, 0.0),
        (0.5,  1.0, 0.0),
        (1.0,  1.0, 1.0),
    ),
    'blue': (
        (0.0,  0.0, 0.0),
        (0.5,  0.0, 0.0),
        (1.0,  1.0, 1.0),
    )
}

e veja cdict['red'][1]; porque , está dizendo que de 0 a 0,5, o vermelho aumenta de 0 a 1, mas depois pula para baixo, de modo que, de 0,5 a 1, o vermelho aumenta de 0,7 a 1. O verde sobe de 0 a 1 à medida que vai de 0 para 0,5, depois salta de volta para 0 e volta para 1 conforme vai de 0,5 para 1.y0 != y1xxxx

row i:   x  y0  y1
               /
              /
row i+1: x  y0  y1

Acima está uma tentativa de mostrar que para xno intervalo x[i]de x[i+1], a interpolação é entre y1[i]e y0[i+1]. Então, y0[0]e y1[-1]nunca são usados.

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap

# Make some illustrative fake data:

x = np.arange(0, np.pi, 0.1)
y = np.arange(0, 2 * np.pi, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.cos(X) * np.sin(Y) * 10

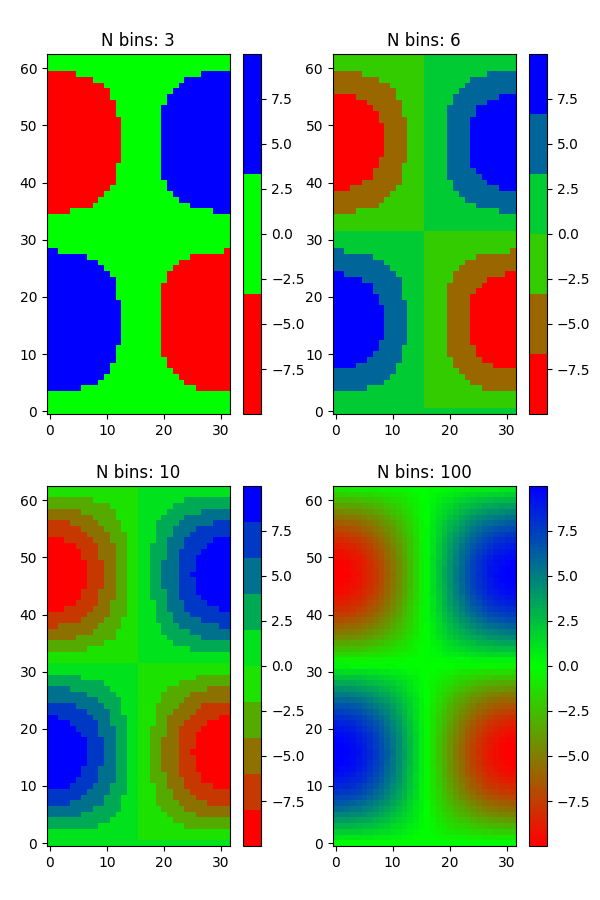
Colormaps de uma lista #

colors = [(1, 0, 0), (0, 1, 0), (0, 0, 1)]  # R -> G -> B
n_bins = [3, 6, 10, 100]  # Discretizes the interpolation into bins
cmap_name = 'my_list'
fig, axs = plt.subplots(2, 2, figsize=(6, 9))
fig.subplots_adjust(left=0.02, bottom=0.06, right=0.95, top=0.94, wspace=0.05)
for n_bin, ax in zip(n_bins, axs.flat):
    # Create the colormap
    cmap = LinearSegmentedColormap.from_list(cmap_name, colors, N=n_bin)
    # Fewer bins will result in "coarser" colomap interpolation
    im = ax.imshow(Z, origin='lower', cmap=cmap)
    ax.set_title("N bins: %s" % n_bin)
    fig.colorbar(im, ax=ax)

N compartimentos: 3, N compartimentos: 6, N compartimentos: 10, N compartimentos: 100

Mapas de cores personalizados #

cdict1 = {
    'red': (
        (0.0, 0.0, 0.0),
        (0.5, 0.0, 0.1),
        (1.0, 1.0, 1.0),
    ),
    'green': (
        (0.0, 0.0, 0.0),
        (1.0, 0.0, 0.0),
    ),
    'blue': (
        (0.0, 0.0, 1.0),
        (0.5, 0.1, 0.0),
        (1.0, 0.0, 0.0),
    )
}

cdict2 = {
    'red': (
        (0.0, 0.0, 0.0),
        (0.5, 0.0, 1.0),
        (1.0, 0.1, 1.0),
    ),
    'green': (
        (0.0, 0.0, 0.0),
        (1.0, 0.0, 0.0),
    ),
    'blue': (
        (0.0, 0.0, 0.1),
        (0.5, 1.0, 0.0),
        (1.0, 0.0, 0.0),
    )
}

cdict3 = {
    'red': (
        (0.0, 0.0, 0.0),
        (0.25, 0.0, 0.0),
        (0.5, 0.8, 1.0),
        (0.75, 1.0, 1.0),
        (1.0, 0.4, 1.0),
    ),
    'green': (
        (0.0, 0.0, 0.0),
        (0.25, 0.0, 0.0),
        (0.5, 0.9, 0.9),
        (0.75, 0.0, 0.0),
        (1.0, 0.0, 0.0),
    ),
    'blue': (
        (0.0, 0.0, 0.4),
        (0.25, 1.0, 1.0),
        (0.5, 1.0, 0.8),
        (0.75, 0.0, 0.0),
        (1.0, 0.0, 0.0),
    )
}

# Make a modified version of cdict3 with some transparency
# in the middle of the range.
cdict4 = {
    **cdict3,
    'alpha': (
        (0.0, 1.0, 1.0),
        # (0.25, 1.0, 1.0),
        (0.5, 0.3, 0.3),
        # (0.75, 1.0, 1.0),
        (1.0, 1.0, 1.0),
    ),
}

Agora usaremos este exemplo para ilustrar 2 maneiras de lidar com mapas de cores personalizados. Primeiro, o mais direto e explícito:

blue_red1 = LinearSegmentedColormap('BlueRed1', cdict1)

Em segundo lugar, crie o mapa explicitamente e registre-o. Assim como o primeiro método, este método funciona com qualquer tipo de mapa de cores, não apenas um LinearSegmentedColormap:

mpl.colormaps.register(LinearSegmentedColormap('BlueRed2', cdict2))
mpl.colormaps.register(LinearSegmentedColormap('BlueRed3', cdict3))
mpl.colormaps.register(LinearSegmentedColormap('BlueRedAlpha', cdict4))

Faça a figura, com 4 subtramas:

fig, axs = plt.subplots(2, 2, figsize=(6, 9))
fig.subplots_adjust(left=0.02, bottom=0.06, right=0.95, top=0.94, wspace=0.05)

im1 = axs[0, 0].imshow(Z, cmap=blue_red1)
fig.colorbar(im1, ax=axs[0, 0])

im2 = axs[1, 0].imshow(Z, cmap='BlueRed2')
fig.colorbar(im2, ax=axs[1, 0])

# Now we will set the third cmap as the default.  One would
# not normally do this in the middle of a script like this;
# it is done here just to illustrate the method.

plt.rcParams['image.cmap'] = 'BlueRed3'

im3 = axs[0, 1].imshow(Z)
fig.colorbar(im3, ax=axs[0, 1])
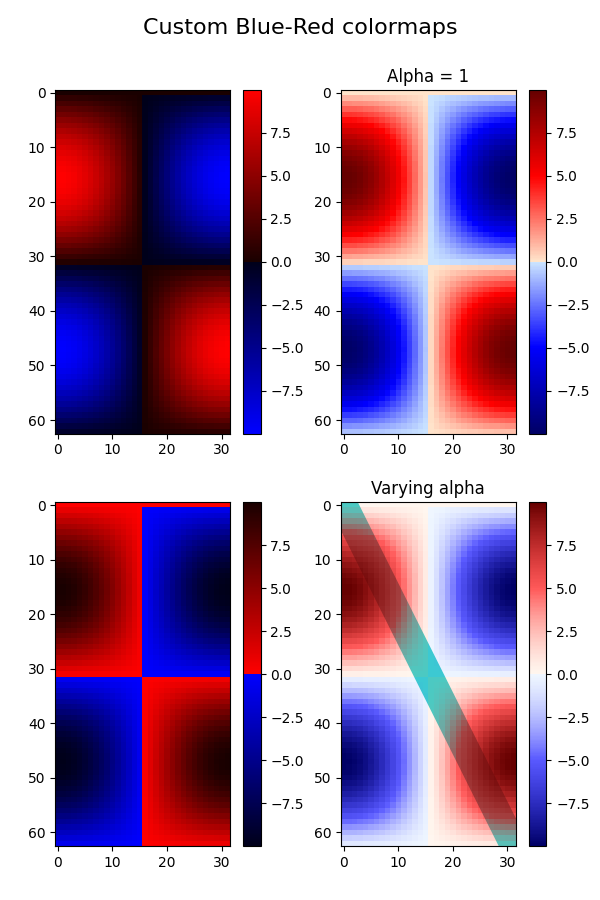
axs[0, 1].set_title("Alpha = 1")

# Or as yet another variation, we can replace the rcParams
# specification *before* the imshow with the following *after*
# imshow.
# This sets the new default *and* sets the colormap of the last
# image-like item plotted via pyplot, if any.
#

# Draw a line with low zorder so it will be behind the image.
axs[1, 1].plot([0, 10 * np.pi], [0, 20 * np.pi], color='c', lw=20, zorder=-1)

im4 = axs[1, 1].imshow(Z)
fig.colorbar(im4, ax=axs[1, 1])

# Here it is: changing the colormap for the current image and its
# colorbar after they have been plotted.
im4.set_cmap('BlueRedAlpha')
axs[1, 1].set_title("Varying alpha")

fig.suptitle('Custom Blue-Red colormaps', fontsize=16)
fig.subplots_adjust(top=0.9)

plt.show()

Mapas de cores azul-vermelho personalizados, alfa = 1, alfa variável

Referências

O uso das seguintes funções, métodos, classes e módulos é mostrado neste exemplo:

Tempo total de execução do script: ( 0 minutos 1,919 segundos)

Galeria gerada por Sphinx-Gallery