Preenchendo a área entre as linhas

Este exemplo mostra como usar fill_betweenpara colorir a área entre duas linhas.

import matplotlib.pyplot as plt
import numpy as np

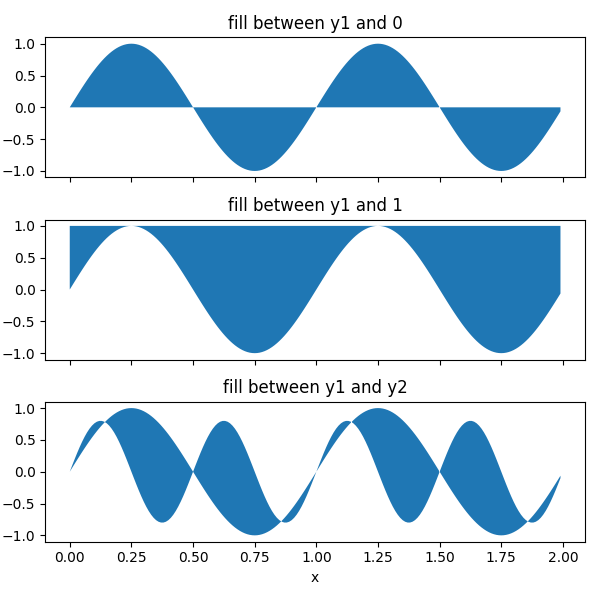
Uso básico

Os parâmetros y1 e y2 podem ser escalares, indicando um limite horizontal nos valores y fornecidos. Se apenas y1 for fornecido, o padrão de y2 é 0.

x = np.arange(0.0, 2, 0.01)
y1 = np.sin(2 * np.pi * x)
y2 = 0.8 * np.sin(4 * np.pi * x)

fig, (ax1, ax2, ax3) = plt.subplots(3, 1, sharex=True, figsize=(6, 6))

ax1.fill_between(x, y1)
ax1.set_title('fill between y1 and 0')

ax2.fill_between(x, y1, 1)
ax2.set_title('fill between y1 and 1')

ax3.fill_between(x, y1, y2)
ax3.set_title('fill between y1 and y2')
ax3.set_xlabel('x')
fig.tight_layout()

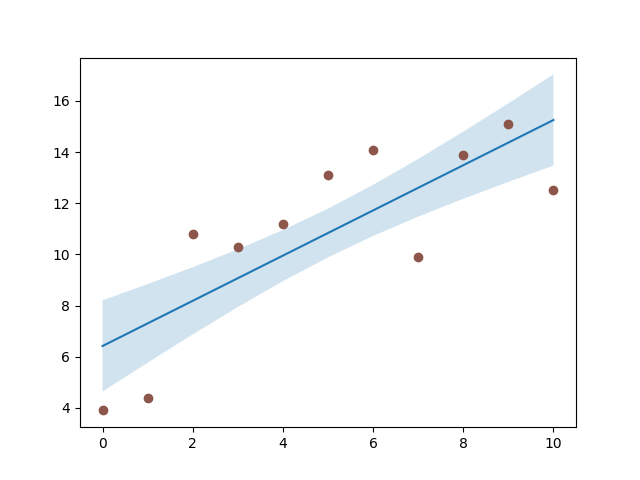
Exemplo: faixas de confiança

Uma aplicação comum fill_betweené a indicação de faixas de confiança.

fill_betweenusa as cores do ciclo de cores como cor de preenchimento. Estes podem ser um pouco fortes quando aplicados para preencher áreas. Portanto, geralmente é uma boa prática clarear a cor tornando a área semitransparente usando alpha .

N = 21
x = np.linspace(0, 10, 11)
y = [3.9, 4.4, 10.8, 10.3, 11.2, 13.1, 14.1,  9.9, 13.9, 15.1, 12.5]

# fit a linear curve an estimate its y-values and their error.
a, b = np.polyfit(x, y, deg=1)
y_est = a * x + b
y_err = x.std() * np.sqrt(1/len(x) +
                          (x - x.mean())**2 / np.sum((x - x.mean())**2))

fig, ax = plt.subplots()
ax.plot(x, y_est, '-')
ax.fill_between(x, y_est - y_err, y_est + y_err, alpha=0.2)
ax.plot(x, y, 'o', color='tab:brown')

[<matplotlib.lines.Line2D object at 0x7f2d0108d030>]

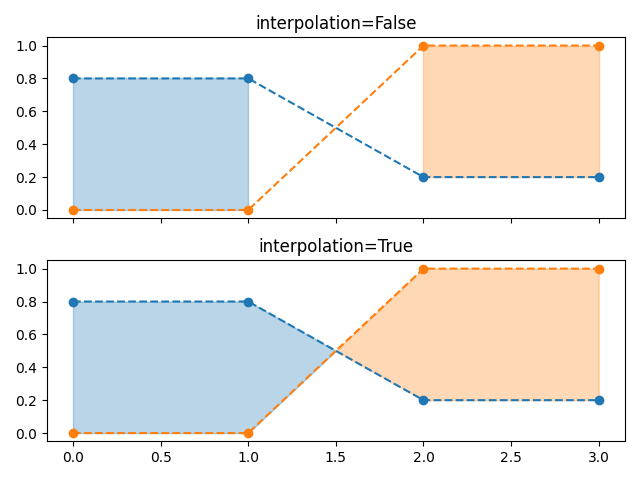
Preenchendo seletivamente regiões horizontais

O parâmetro where permite especificar os intervalos x a serem preenchidos. É uma matriz booleana com o mesmo tamanho que x .

Apenas intervalos x de sequências verdadeiras contíguas são preenchidos. Como resultado, o intervalo entre os valores True e False vizinhos nunca é preenchido. Isso geralmente é indesejado quando os pontos de dados devem representar uma quantidade contígua. Portanto, é recomendável definir interpolate=Truea menos que a distância x dos pontos de dados seja suficientemente fina para que o efeito acima não seja perceptível. A interpolação aproxima a posição x real na qual a condição where mudará e estende o preenchimento até lá.

x = np.array([0, 1, 2, 3])
y1 = np.array([0.8, 0.8, 0.2, 0.2])
y2 = np.array([0, 0, 1, 1])

fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)

ax1.set_title('interpolation=False')
ax1.plot(x, y1, 'o--')
ax1.plot(x, y2, 'o--')
ax1.fill_between(x, y1, y2, where=(y1 > y2), color='C0', alpha=0.3)
ax1.fill_between(x, y1, y2, where=(y1 < y2), color='C1', alpha=0.3)

ax2.set_title('interpolation=True')
ax2.plot(x, y1, 'o--')
ax2.plot(x, y2, 'o--')
ax2.fill_between(x, y1, y2, where=(y1 > y2), color='C0', alpha=0.3,
                 interpolate=True)
ax2.fill_between(x, y1, y2, where=(y1 <= y2), color='C1', alpha=0.3,
                 interpolate=True)
fig.tight_layout()

Observação

Lacunas semelhantes ocorrerão se y1 ou y2 forem matrizes mascaradas. Como os valores ausentes não podem ser aproximados, a interpolação não tem efeito nesse caso. As lacunas em torno dos valores mascarados só podem ser reduzidas adicionando mais pontos de dados próximos aos valores mascarados.

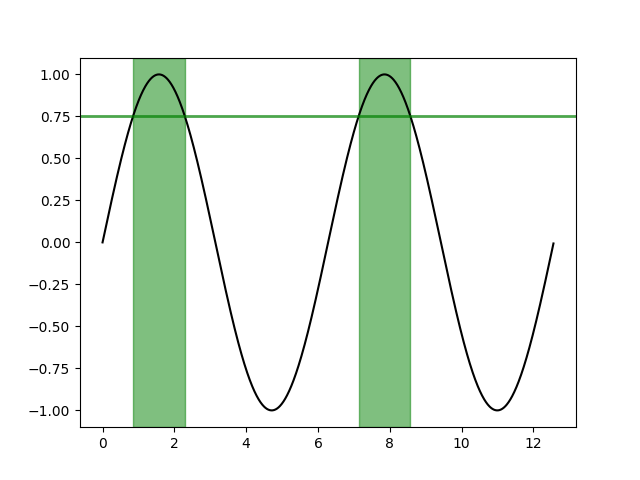
Marcando seletivamente regiões horizontais em todo o eixo

O mesmo mecanismo de seleção pode ser aplicado para preencher toda a altura vertical dos eixos. Para ser independente dos limites y, adicionamos uma transformação que interpreta os valores x em coordenadas de dados e os valores y em coordenadas de eixos.

O exemplo a seguir marca as regiões nas quais os dados y estão acima de um determinado limite.

fig, ax = plt.subplots()
x = np.arange(0, 4 * np.pi, 0.01)
y = np.sin(x)
ax.plot(x, y, color='black')

threshold = 0.75
ax.axhline(threshold, color='green', lw=2, alpha=0.7)
ax.fill_between(x, 0, 1, where=y > threshold,
                color='green', alpha=0.5, transform=ax.get_xaxis_transform())

<matplotlib.collections.PolyCollection object at 0x7f2d00e640a0>

Referências

O uso das seguintes funções, métodos, classes e módulos é mostrado neste exemplo:

• matplotlib.axes.Axes.fill_between/matplotlib.pyplot.fill_between

• matplotlib.axes.Axes.get_xaxis_transform