Observação
Clique aqui para baixar o código de exemplo completo
Demonstração de seta #
Três maneiras de desenhar setas para codificar a "força" da seta (por exemplo, probabilidades de transição em um modelo de Markov) usando comprimento, largura ou alfa (opacidade) da seta.
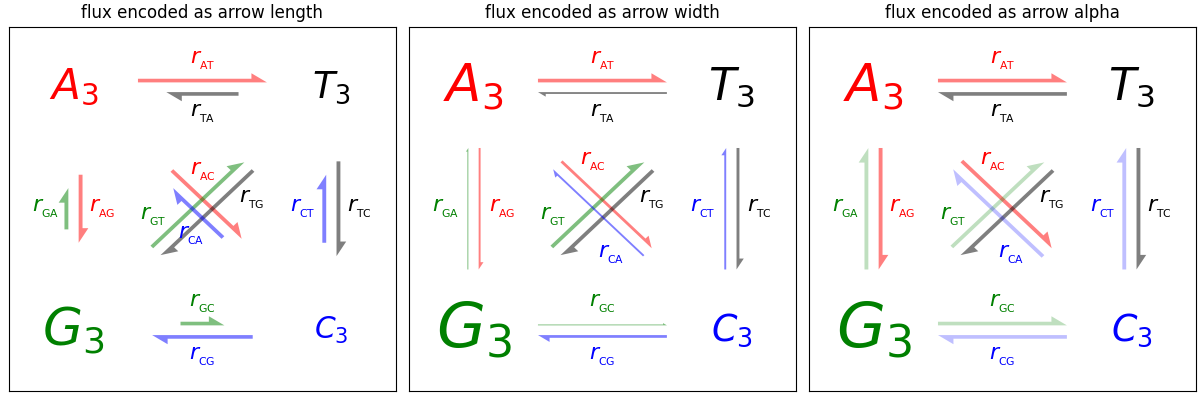
import itertools
import matplotlib.pyplot as plt
import numpy as np
def make_arrow_graph(ax, data, size=4, display='length', shape='right',
max_arrow_width=0.03, arrow_sep=0.02, alpha=0.5,
normalize_data=False, ec=None, labelcolor=None,
**kwargs):
"""
Makes an arrow plot.
Parameters
----------
ax
The axes where the graph is drawn.
data
Dict with probabilities for the bases and pair transitions.
size
Size of the plot, in inches.
display : {'length', 'width', 'alpha'}
The arrow property to change.
shape : {'full', 'left', 'right'}
For full or half arrows.
max_arrow_width : float
Maximum width of an arrow, in data coordinates.
arrow_sep : float
Separation between arrows in a pair, in data coordinates.
alpha : float
Maximum opacity of arrows.
**kwargs
`.FancyArrow` properties, e.g. *linewidth* or *edgecolor*.
"""
ax.set(xlim=(-0.25, 1.25), ylim=(-0.25, 1.25), xticks=[], yticks=[],
title=f'flux encoded as arrow {display}')
max_text_size = size * 12
min_text_size = size
label_text_size = size * 4
bases = 'ATGC'
coords = {
'A': np.array([0, 1]),
'T': np.array([1, 1]),
'G': np.array([0, 0]),
'C': np.array([1, 0]),
}
colors = {'A': 'r', 'T': 'k', 'G': 'g', 'C': 'b'}
for base in bases:
fontsize = np.clip(max_text_size * data[base]**(1/2),
min_text_size, max_text_size)
ax.text(*coords[base], f'${base}_3$',
color=colors[base], size=fontsize,
horizontalalignment='center', verticalalignment='center',
weight='bold')
arrow_h_offset = 0.25 # data coordinates, empirically determined
max_arrow_length = 1 - 2 * arrow_h_offset
max_head_width = 2.5 * max_arrow_width
max_head_length = 2 * max_arrow_width
sf = 0.6 # max arrow size represents this in data coords
if normalize_data:
# find maximum value for rates, i.e. where keys are 2 chars long
max_val = max((v for k, v in data.items() if len(k) == 2), default=0)
# divide rates by max val, multiply by arrow scale factor
for k, v in data.items():
data[k] = v / max_val * sf
# iterate over strings 'AT', 'TA', 'AG', 'GA', etc.
for pair in map(''.join, itertools.permutations(bases, 2)):
# set the length of the arrow
if display == 'length':
length = (max_head_length
+ data[pair] / sf * (max_arrow_length - max_head_length))
else:
length = max_arrow_length
# set the transparency of the arrow
if display == 'alpha':
alpha = min(data[pair] / sf, alpha)
# set the width of the arrow
if display == 'width':
scale = data[pair] / sf
width = max_arrow_width * scale
head_width = max_head_width * scale
head_length = max_head_length * scale
else:
width = max_arrow_width
head_width = max_head_width
head_length = max_head_length
fc = colors[pair[0]]
cp0 = coords[pair[0]]
cp1 = coords[pair[1]]
# unit vector in arrow direction
delta = cos, sin = (cp1 - cp0) / np.hypot(*(cp1 - cp0))
x_pos, y_pos = (
(cp0 + cp1) / 2 # midpoint
- delta * length / 2 # half the arrow length
+ np.array([-sin, cos]) * arrow_sep # shift outwards by arrow_sep
)
ax.arrow(
x_pos, y_pos, cos * length, sin * length,
fc=fc, ec=ec or fc, alpha=alpha, width=width,
head_width=head_width, head_length=head_length, shape=shape,
length_includes_head=True,
**kwargs
)
# figure out coordinates for text:
# if drawing relative to base: x and y are same as for arrow
# dx and dy are one arrow width left and up
orig_positions = {
'base': [3 * max_arrow_width, 3 * max_arrow_width],
'center': [length / 2, 3 * max_arrow_width],
'tip': [length - 3 * max_arrow_width, 3 * max_arrow_width],
}
# for diagonal arrows, put the label at the arrow base
# for vertical or horizontal arrows, center the label
where = 'base' if (cp0 != cp1).all() else 'center'
# rotate based on direction of arrow (cos, sin)
M = [[cos, -sin], [sin, cos]]
x, y = np.dot(M, orig_positions[where]) + [x_pos, y_pos]
label = r'$r_{_{\mathrm{%s}}}$' % (pair,)
ax.text(x, y, label, size=label_text_size, ha='center', va='center',
color=labelcolor or fc)
if __name__ == '__main__':
data = { # test data
'A': 0.4, 'T': 0.3, 'G': 0.6, 'C': 0.2,
'AT': 0.4, 'AC': 0.3, 'AG': 0.2,
'TA': 0.2, 'TC': 0.3, 'TG': 0.4,
'CT': 0.2, 'CG': 0.3, 'CA': 0.2,
'GA': 0.1, 'GT': 0.4, 'GC': 0.1,
}
size = 4
fig = plt.figure(figsize=(3 * size, size), constrained_layout=True)
axs = fig.subplot_mosaic([["length", "width", "alpha"]])
for display, ax in axs.items():
make_arrow_graph(
ax, data, display=display, linewidth=0.001, edgecolor=None,
normalize_data=True, size=size)
plt.show()
Tempo total de execução do script: ( 0 minutos 1,045 segundos)