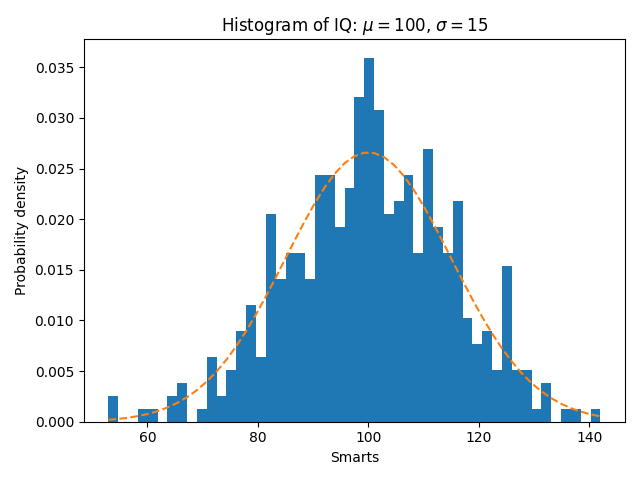
Algumas características da função histograma (hist) #

Além do histograma básico, esta demonstração mostra alguns recursos opcionais:

Configurando o número de compartimentos de dados.
O parâmetro de densidade , que normaliza as alturas dos compartimentos para que a integral do histograma seja 1. O histograma resultante é uma aproximação da função de densidade de probabilidade.

A seleção de diferentes contagens e tamanhos de compartimentos pode afetar significativamente a forma de um histograma. Os documentos do Astropy têm uma ótima seção sobre como selecionar esses parâmetros.

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(19680801)

# example data
mu = 100  # mean of distribution
sigma = 15  # standard deviation of distribution
x = mu + sigma * np.random.randn(437)

num_bins = 50

fig, ax = plt.subplots()

# the histogram of the data
n, bins, patches = ax.hist(x, num_bins, density=True)

# add a 'best fit' line
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
     np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
ax.plot(bins, y, '--')
ax.set_xlabel('Smarts')
ax.set_ylabel('Probability density')
ax.set_title(r'Histogram of IQ: $\mu=100$, $\sigma=15$')

# Tweak spacing to prevent clipping of ylabel
fig.tight_layout()
plt.show()

$Histograma de QI: $\mu=100$, $\sigma=15$$

Referências

O uso das seguintes funções, métodos, classes e módulos é mostrado neste exemplo:

Galeria gerada por Sphinx-Gallery